Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting

1 Summary

Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting [1]

本文提出了一种基于蓄水池采样的流式重采样方法，旨在提高 many-lights 场景下，光追计算直接光照过程中的重要性采样的效率。

在以往的重要性采样方法中，

  1. IS：最基础的采用单一分布采样技术在复杂被积函数下有较大方差，如多项乘积形式的渲染方程仅能与其中一项成比例。
  2. MIS：再到能够结合多种采样策略的多重重要性采样，其以一定权重对来自不同采样策略的样本进行无偏结合，本质上使用多个简单的源分布的线性组合来拟合复杂的目标分布。结合过程与乘积形式的渲染方程有一定偏差，且复杂度较高，每次采样一个目标分布的样本都需要对所有源分布生成一批样本。
  3. RIS：重采样重要性采样是先从易采样的源分布中采样一批候选样本，再以一定（目标分布/源分布）权重从候选样本中挑选出近似于目标分布的样本。而在蒙特卡洛中矫正这种近似，将积分采样分布矫正为 (目标分布/权重均值)。这种重采样过程从概率角度看是采样后的采样，是一种概率分布上的乘积形式，更接近渲染方程的乘积形式。但是单一源分布对最终的目标分布影响很大，如果在重采样过程中引入多重重要性采样，会得到平方级的开销增长。
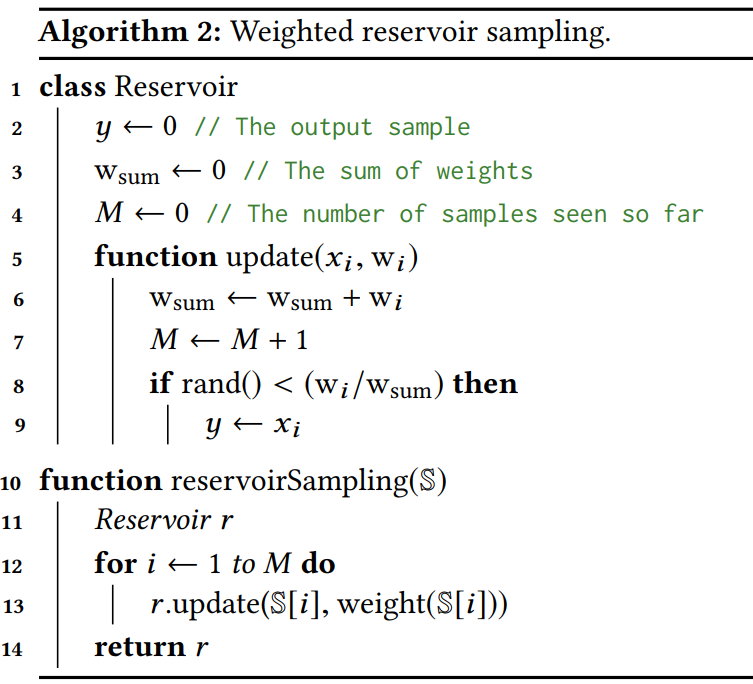
  4. WRS：基于权重的蓄水池采样可以不断接收输入样本来优化自身样本的分布，其所需输入为样本及其关联权重，更新过程为在保持自身分布不变的条件下，来选择是否替换自身样本。具体来说，接收输入样本 $x_{m+1}$ 时，以概率 $\frac{w_{m+1}}{\sum w_i}$ 来决定是否替换已有样本 $x_i$，这样的替换过程仍然保持了蓄水池中样本的分布为 (自身权重/权重和)。蓄水池采样过程是一种流式的更新，即可以不断输入新样本，更新内部数据：$\mathrm{w}_{sum},M$ 以及输出样本 $y$

作者基于 RIS 理论，设计蓄水池采样的更新权重，将二者结合，提出了高效的基于蓄水池采样的流式重采样方法。对于着色点像素的 reservoir 而言，可以不断接收来自源分布的候选样本，越来越接近目标分布。作者基于与当前像素分布相近的reservoir也可用来复用提升采样率，提出了在时空间上，对reservoir的直接复用算法。reservoir之间的复用过程，输入的是相邻/历史像素的reservoir，因此reservoir不需要维护昂贵的input stream，仅需要当前状态即可。这两种reservoir更新过程如下：

  • 接收来自源分布的候选样本的更新：蓄水池的更新权重设计为 (目标分布/源分布)。基于 RIS 理论，最终蓄水池输出样本 $y$ 以及对应蒙特卡洛权重 $\large \frac{\mathrm{w}_{sum}/M}{\hat{p}(y)}$

  • 复用其它reservoir的更新：reservoir 之间的复用，是对reservoir当前状态的复用过程，即考虑输入reservoir的 $\mathrm{w}{sum},M$。 而将复用reservoir $q’$的分布作为源分布，当前reservoir $q$ 的分布作为目标分布，使用 $\large \frac{\hat{p}q(r{q’}{{.}}y)}{\hat{p}{q’}(r{q’}{{.}}y)}$ 来矫正权重，更新权重为，
    $$
    r    {q’}{{.}}\mathrm{w}{sum} \cdot \frac{\hat{p}q(r{q’}{{.}}y)}{\hat{p}{q’}(r_{q’}{{.}}y)}=\hat{p}q(r{q’}{{.}}y) \cdot r_{q’}{{.}}W \cdot r{q’}{_{.}}M
    $$

复用reservoir过程中，spatial reuse 可以多次调用，temporal reuse 通过motion vector找到对应的历史像素。但由于目标分布选取的是 unshadowed path contribution，随着样本数增加，visibility带来的噪声会越明显，对此作者选择在时空间复用前，先对复用reservoir样本trace shadow ray，丢弃遮挡项。

2 Background

本论文将光源视为场景中的发光几何体，因此 many-lights 下的渲染方程为：着色点 $y$ 在方向 $\vec{\omega}$ 所反射的 radiance $L$ 是对所有发光表面 $A$ 的积分：
$$
L(y,\vec{\omega}) = \int_A \rho(y,\vec{yx}\leftrightarrow\vec{\omega})L_e(x\rightarrow y)G(x\leftrightarrow y)V(x\leftrightarrow y) \space dA_x \tag{1} \label{render equation}
$$
其中，$\vec{\omega}$ 是观察方向，与相机相关；$\rho$ 与着色点 $y$ 的材质有关，论文中指 BSDF；$L_e$ 是光源表面一点 $x$ 到着色点 $y$ 方向上发出的 radiance；$G$ 几何项，包含了 inverse squared distance 和反射方向与入射方向的余弦项。

对渲染方程的表示进行一些符号简化，被积函数简化为 $f(x)$，积分微元 $dx$，有渲染方程的简化形式：
$$
L=\int_A f(x)\space dx,\quad where \space f(x)\equiv\rho(x)\cdot L_e(x)\cdot G(x)\cdot V(x) \tag{2} \label{simple render equation}
$$

2.1 Importance Sampling(IS)

蒙特卡洛重要性采样使用单一分布进行采样，使得样本集中在被积函数的关键区域，最优采样分布是与被积函数成比例。使用蒙特卡洛重要性采样方法估计 $\eqref{simple render equation}$ 式积分，从 source PDF $p(x_i)$ 中进行 $N$ 次采样，得到 $N$ 个样本，$\eqref{simple render equation}$ 积分的估计量为：
$$
L \approx \langle L \rangle_{IS}^N =\frac{1}{N}\sum\limits_{i=1}^N \frac{f(x_i)}{p(x_i)} \tag{3} \label{IS MC}
$$
其中如果在 $f(x)$ 非零时，$p(x)$ 都为正，IS 则为无偏估计；并且可以通过选取与 $f(x)$ 相关的 $p(x)$ 形式，来降低方差。

2.2 Multiple Importance Sampling(MIS)

由于 $f(x)$ 的复杂性（包含多项），直接采样与 $f(x)$ 成比例（相关）的分布是不可实行的，而 IS 通常采样与 $f(x)$ 中单项成比例的分布，例如 $\rho$ BSDF、$L_e$ 等，而单一采样策略（如仅BRDF采样或者仅光源采样）会无法高兴覆盖所有重要区域，导致较高的方差。

多重重要性采样定义 $M$ 个采样策略 $p_s$ (概率分布)，MIS 从每个采样策略 $s$ 中采样出 $N_s$ 个样本，再将这些来自不同分布的样本以一定权重函数组合到一个 weighted-estimator 中，如下：
$$
L\approx \langle L\rangle_{MIS}^{M,N}=\sum\limits_{s=1}^M\frac{1}{N_s}\sum\limits_{i=1}^{N_s}w_s(x_i)\frac{f(x_i)}{p(x_i)} \tag{4}\label{MIS MC}
$$
其中，只要权重 $w_s$ 可以组成一个归一化整体，MIS 就是无偏估计，即 $\sum^M_{s=1}w_s(x)=1$。一种流行且较好的启发式选择为 $\Large w_s(x)=\frac{N_s p_s(x)}{\sum_j N_jp_j(x)}$，等价于采样 $M$ 个独立采样策略的混合分布。

2.3 Resample Importance Sampling(RIS)

由 $\eqref{MIS MC}$ 可以看出，MIS 需要对每个采样策略采样一批样本，是对着色项的线性组合的采样，开销较高。而另一种可选的采样策略是对其中一些项的乘积进行近似成比例地采样。

重采样重要性采样的策略是先从易于采样的源分布中采样一批候选样本，再在候选样本中以一定权重进行重采样来接近目标分布。具体过程：RIS 从非最优但高效的 source PDF $p$ 中生成 $M\geq 1$ 个候选样本 $\boldsymbol{x}={x_1,\cdots,x_M}$，如 $p \propto L_e $。然后从这个候选池中使用以下离散概率分布进行随机选取 $z\in{1,\cdots,M}$，
$$
p(z\mid \boldsymbol{x})=\frac{\mathrm{w}(x_z)}{\sum^M_{i=1}\mathrm{w}(x_i)} \quad with \quad \mathrm{w}(x)=\frac{\hat{p}(x)}{p(x)} \tag{5}\label{discrete PDF}
$$
其中，$\hat{p}(x)$ 为期望得到的 target PDF，例如无法直接采样的分布 $\hat{p}\propto \rho\cdot L_e \cdot G$。

对一些项的乘积成比例的策略：重采样是先从单一分布生成候选样本，再从候选样本重采样，也就是采样后的采样，在数学概率形式上类似于概率分布的乘积

被选中的样本为 $y\equiv x_z$，得到的1-sample RIS 估计量有
$$
L\approx \langle L \rangle^{1,M}{RIS} = \frac{f(y)}{\hat{p}(y)}\cdot\left(\frac{1}{M}\sum\limits^M{j=1}\mathrm{w}(x_j)\right) \tag{6} \label{1-sample RIS}
$$

对 $\eqref{1-sample RIS}$ 的理解：RIS 一次采样目的是得到一个 target PDF $\hat{p}$ 的样本 $y$，但 $y$ 的实际分布只是近似于 target PDF $\hat{p}$。因此通过括号内的因子（即候选样本权重的均值）来进行校正。

多次执行 RIS，然后取平均，可以得到一个 N-sample RIS 估计量：
$$
L \approx\langle L\rangle^{M,N}{RIS}=\frac{1}{N}\sum\limits^N{i=1}\left(\frac{f(y_i)}{\hat{p}(y_i)}\cdot \left(\frac{1}{M}\sum^M_{j=1}\mathrm{w}(x_{ij})\right)\right) \tag{7} \label{N-sample RIS}
$$

2.3.1 1-sample RIS 算法流程

在 $M,N\geq 1$ 并且 $f$ 非零时，$p,\hat{p}$ 都为正，RIS 则为无偏估计。理论上 $M$ 和 $N$ 存在与方差有关的最优比，但实际中，这个比值难以事先预知。本文中采用简单形式 $N=1$，即 1-sample RIS。有算法流程：

  1. 预设 source PDF $p$，文中实验将其设为在面光源上的面积采样分布；target PDF $\hat{p}$，文中实验设置为 unshadowed path contribution 部分，即 $\rho \cdot L_e\cdot G$，不包含 visibility 项

  2. 设置初始为空的权重列表 $\textup{W}$，初始为 $0$ 的权重累积和 $\textup{w}_{sum}$，初始为空的候选样本列表 $\boldsymbol{x}$

  3. 对 source PDF $p$ 进行 $M$ 次采样：

    • 第 $i$ 次采样的随机样本为 $x_i$，放入候选样本列表 $\boldsymbol{x}$

    • 计算样本 $x_i$ 的权重 $\mathrm{w}_i=\Large \frac{\hat{p}(x_i)}{p(x_i)}$，并放入权重列表 $\mathrm{W}$

    • 累积权重和 $\mathrm{w}{sum}=\mathrm{w}{sum}+\mathrm{w}_i$

  4. 对候选样本权重进行归一化：$\mathrm{w}_i= \Large \frac{\mathrm{w}i}{\mathrm{w}{sum}}$

  5. 将归一化权重作为候选样本的概率分布，采样候选样本列表得到最终选出的样本 $y=x_z$

  6. 返回选出的样本 $y=x_z$ 以及本次 RIS 的候选样本的权重累积和 $\textup{w}_{sum}$

假设像素 $q$ 对应 target PDF $\hat{p}(q)$，以及其渲染方程积分 $f_q$，1-sample RIS 算法伪代码如下：

image-20220717215808514
算法 1

$\eqref{1-sample RIS}$ 式的计算需要候选样本数量 $M$，这是算法输入，是已知的；$\mathrm{w}_{sum}$，算法输出；$\hat{p}(y)$，$y$ 是算法选出的样本，$\hat{p}$ 是预设 target PDF，本文使用的是代入样本到被积函数后的颜色转为亮度。

2.3.2 结合 MIS 的 RIS

前述假设仅使用单一源分布 $p$，只要 $p$ 在 $\hat{p}$ 非零的区域始终为正，随着 $M \rightarrow \infty$，$y \rightarrow \hat{p}$。但实际问题会涉及多种采样技术，例如BSDF采样或光源采样，源分布的心态会影响目标分布的收敛速度。[3] 证明了如何在 RIS 中通过 MIS 整合多种竞争性采样技术以降低方差，但MIS形式的计算成本会随着采样技术数量呈平方级增长。本文通过时空间复用来显著增加候选样本数量，提出一种新的 MIS 方法，显著降低计算复杂度。

2.4 Weighted Reservoir Sampling(WRS)

WRS 是一类从一个 stream ${x_1,x_2,\cdots,x_M}$ 中通过一遍操作来随机采样 $N$ 个元素的算法，该 stream 数据中每个元素 $x_i$ 都关联一个权重 $\textup{w}(x_i)$，$x_i$ 被选中的概率为
$$
P_i = \frac{\mathrm{w}(x_i)}{\sum^M_{j=1}\mathrm{w}(x_j)} \tag{8} \label{reservoir CDF}
$$
Reservoir sampling 对每个元素只进行一次操作，仅需要 $N$ 个元素保留在内存中，并且 stream 的长度 $M$ 不必事先预知。Reservoir sampling 算法，分为有放回采样与无放回采样，由于蒙特卡洛积分积分的采样通常是相互独立的，因此本论文只考虑较为简单的有放回采样算法。

Reservoir sampling 按照 input stream 的次序来处理其中的元素，保存一个具有 $N$ 个样本的 reservoir。当处理数据流中的新元素时，算法通过更新规则保持蓄水池中的分布不变。具体的更新操作为：

在处理了 m 个样本之后，样本 $x_i$ 在 reservoir 出现的概率为 $\textup{w}(x_i)/\sum^m_{j=1}\textup{w}(x_j)$。处理下一个新元素 $x_{m+1}$ 的更新规则为，使用下一个样本 $x_{m+1}$ 以以下概率随机替换 reservoir 中样本 $x_i$ ：
$$
\frac{\mathrm{w}(x_{m+1})}{\sum^{m+1}{j=1}\mathrm{w}(x_j)}
$$
因此任意之前的样本 $x_i$ 在 reservoir 内的概率(即已在 reservoir 中，且不会被下一个样本替换掉的概率)为：
$$
\frac{\mathrm{w}(x_i)}{\sum^m{j=1}\mathrm{w}(x_j)}\left(1-\frac{\mathrm{w}(x_{m+1})}{\sum^{m+1}{j=1}\mathrm{w}(x_j)}\right)=\frac{\mathrm{w}(x_i)}{\sum^{m+1}{j=1}\mathrm{w}(x_j)}
$$

可以看出 N 个样本的 reservoir 接收到一个新元素的更新规则是，逐个样本执行更新规则

观察 $\eqref{reservoir CDF}$ 中给出的 reservoir CDF 可知，在处理过一个新的元素后 reservoir 中元素的概率分布依然不变。N=1 时的 WRS 算法如下：

image-20220717215902454

3 Streaming RIS With Spatiotemporal Reuse

RIS 算法对多个 source PDF 的样本进行重采样，重采样的概率分布结合了被积函数的(unshadowed) target PDF 以及源分布，而 target PDF 可以近似为渲染方程 $\eqref{simple render equation}$ 的被积函数每一项对应分布的乘积形式，这种乘积形式要比 MIS 的线性组合形式更接近被积函数的真实分布。因此，RIS 最终选出的样本可近似看作一次 MIS 采样(包含多种采样策略)的样本，且理论上更优。

WRS 算法能够高效地维护一个 reservoir，在保持 reservoir 中原有样本所服从分布不变的情况下，不断纳入新的随机样本，使得 reservoir 样本不断逼近目标估计量的期望值。

理论上，对 RIS 应用 WRS 可以得到一个使 RIS 样本不断逼近期望值的高效算法，当然由于本文的 target PDF 选取 unshadowed path contribution，最终会由于 visibility 无法继续提高 RIS 样本。下面介绍如何应用 WRS 算法，从而得到 Streaming RIS 算法。

3.1 Streaming RIS Using Reservoir Sampling

RIS 算法为每个像素 $q$ 独立地生成候选样本，再在候选样本中以 target PDF $\hat{p}_q$ 重新采样，选出最终的样本。对 RIS 可以直接应用 WRS 算法，RIS 选出的样本及其对应的权重，可以直接用于 WRS 算法更新其 reservoir。论文中，通过均匀采样 emitter 的面积，并且使用无阴影的路径的贡献 $\hat{p}(x)=\rho(x)\cdot L_e(x)\cdot G(x)$ 作为 target distribution，仅对 reservoir 中的 $N$ 个样本进行 trace shadow ray。Streaming RIS 算法如下，

image-20220717215920480
算法 3

这里每次更新 reservoir ：候选样本 $x_i$ 及其在 $\eqref{discrete PDF}$ 权重中的 $\Large \textup{w}_{i}=\frac{\hat{p}(x_i)}{p(x_i)}$。

3.2 Spatiotemporal Reuse

3.2.1 复用 reservoir

Reservoir 样本累积了目前见过的所有样本信息，如果可以基于某些策略(如接下来的Spatiotemporal)，选择与当前像素样本分布相似的某些像素的 reservoir，再与当前像素的 reservoir 进行结合复用，就能大幅提高当前像素的采样率。

一种易想到的简单复用方式使用 2-pass 算法：第一个 pass 先为每一个像素生成其候选样本；第二个 pass 再结合自身与其周围像素的候选样本，进行重采样。但这种方式带来的内存开销非常大，需要存储每个像素的候选样本，即 input stream (如前述算法中 $M$ 个)。

为了规避内存开销问题，论文使用了 Reservoir sampling 的一个重要性质，该性质可以在不访问其他 reservoir 的 input stream 的条件下，结合多个 reservoir。如果多个 reservoir 中样本分布相似，同样可以将多个 reservoir 输入到一个新的 reservoir 中，这个新的 reservoir 汇集了所有输入 reservoir 的样本信息，并且由于相似的样本分布，而得到采样率/质量更高的样本。

以两个 reservoir 为例：每个 reservoir 当前的状态包含当前选择的样本 $y$ 以及其 sum weight $\textup{w}_{sum}$，作为一个新的 reservoir 的输入，重采样出一个结合两个输入 reservoir 的新样本和新权重。这种方式只需要访问 reservoir 的当前状态，避免了存储 input stream 的开销，但结果在数学形式上等同于在两个 reservoir 的 input streams 重采样。

复用 reservoir 只是与当前 reservoir 的样本分布相似，但不完全相同，因此需要根据样本分布调整权重。假设 $q$ 为当前像素，$q’$ 为复用像素，论文中将新的 reservoir 中的样本权重使用 $\hat{p}q(r.y)/\hat{p}{q’}(r.y)$ 进行调整，采用 [算法 3](#Algo 3) 中的符号得到最终新的权重为 $\hat{p}_q(r.y)\cdot r.W \cdot r.M$。对于任意数量的 reservoir 都可以以这种方式结合，下面是 $k$ 个 reservoir 结合的算法，只有 O(k) 的复杂度：

image-20220717215937128
算法 4

算法理解：

  • [算法3](#Algo 3)中给出了reservoir接收一个来自源分布样本的更新过程，在结合多个reservoir时，需要考虑reservoir的已输入的候选样本数量 $M$，因此权重采用的是reservoir目前为止的权重之和 $\mathrm{w}_{sum}$

  • 在复用 reservoir 样本时，新的 reservoir 的 source PDF 就是输入 reservoir 样本的分布。具体来说，权重调整系数来自于重采样理论 $\eqref{discrete PDF}$ 中的权重 $\frac{\hat{p}}{p}$，此时复用样本的分布 $\hat{p}_{q’}$ 作为源分布，当前像素reservoir的目标分布作为目标分布 $\hat{p}_q$。

  • ${r_1,\cdots,r_k}$ 为复用样本 $q’$ 的reservoir，由[算法3](#Algo 3)可知，
    $$
    r_i{{.}}W=\frac{1}{\hat{p}{q’}(r_i{{.}}y)}\cdot\left(\frac{r_i{{.}}\mathrm{w}{sum}}{r_i{{.}}M}\right)
    $$

  • 考虑到权重调整，得到最终的更新权重为
    $$
    \begin{align}
    &r_i{{.}}\mathrm{w}{sum} \cdot \frac{\hat{p}q(r_i{{.}}y)}{\hat{p}{q’}(r_i{{.}}y)} \
    &=\underbrace{r_i{{.}}W \cdot r_i{{.}}M \cdot \hat{p}{q’}(r_i{{.}}y)}{r_i{{.}}\mathrm{w}{sum}} \cdot \frac{\hat{p}q(r_i{{.}}y)}{\hat{p}{q’}(r_i{{.}}y)}\
    &=\hat{p}q(r_i{{.}}y) \cdot r_i{    {.}}W \cdot r_i{_{.}}M
    \end{align}
    $$

下面介绍，选用那些像素的 reservoir 来增强当前像素。

3.2.2 Spatial Reuse

空间复用基于一种观察：相邻像素的 target PDFs 通常存在显著联系，通常具有相似的 Geometry 和 BSDF。因此可以结合相邻像素的 RIS 候选样本来增加自身的 RIS 候选样本数量。

空间复用相邻像素的 reservoir 的步骤如下：

  1. 使用 [算法 3](#Algo 3) RIS(q) 为每个像素生成 $M$ 个候选样本，并将 reservoir 的结果存储在 image-sized buffer 中。
  2. 每个像素选取 $k$ 个邻居像素，并使用 [算法 4](#Algo 4) 结合 $k$ 个邻居像素的 reservoirs 以及自身的 reservoir。

每像素的复杂度为 $O(k+M)$，但产生了 $k\cdot M$ 个候选样本。Spatial Reuse 可以重复多次执行，其中每次都是上个 reuse pass 的输出。对于执行了 $n$ 次空间复用迭代，假设每次迭代都复用不同的相邻像素，那么时间复杂度为 $O(kn+M)$，但产生了 $k^n\cdot M$ 个候选样本。

注意，虽然空间复用可以大幅增多候选样本，即采样率，进而提高图像质量，但这种提升不会随着迭代次数增加而一直增加下去。直至迭代次数多到相邻像素的像素信息被全部利用到，图像质量不再提升。

3.2.3 Temporal Reuse

上一帧的像素同样可以提供可复用的候选样本。当完成绘制一帧时，将当前帧的像素的 reservoir 结果存入历史帧信息中。在下一帧时利用 motion vector 找到像素的对应关系，复用对应像素的历史 reservoir。

3.2.4 Visibility Reuse

不幸的是，即使有无限数量的候选样本，RIS 也无法达到无噪声的图像质量。尽管理论上，$M\rightarrow \infty$ 时，reservoir 样本的分布趋向于 target PDF $\hat{p}$，但 $\hat{p}$ 并没有完美采样渲染方程的被积函数。因为，在实际中，$\hat{p}$ 通常设置为了无阴影的 path contribution，当 $M$ 不断增大时，由于 visibility 项噪声会越来越明显，并且 visibility 噪声会表现的非常严重。论文为了解决这一问题，同样对 visibility 进行复用。

在进行 spatial reuse 或者 temporal reuse 之前，先**对每个像素的 reservoir 选择的样本 $y$ 进行 visibility 评估。如果 $y$ 被遮挡，则丢弃该 reservoir，即被遮挡的样本不会传递给其相邻像素。**visibility 评估需要对当前像素向复用的 reservoir 样本发射 shadow ray。

3.2.5 完整算法描述

将上述过程全部考虑进来，得到完整的算法流程：

  1. 首先为每个像素生成 $M$ 个 light candidates，进行重采样，选出最终的样本
  2. 对选出的样本进行 visibility 测试，从中丢弃掉被遮挡的样本
  3. 结合每个像素的 reservoir 和上一帧的对应像素的 reservoir
  4. 执行 $n$ 次空间复用迭代，利用附近 $k$ 个像素的 reservoirs

算法伪代码如下所示：

image-20220717215954040

4 Eliminating Bias in Multi-Distribution RIS

虽然上一部分引入复用样本，提升了图片质量，但由于每个像素都具有不同的积分区域和 target PDF，复用会引入潜在的偏差，导致蒙特卡洛积分成为有偏估计。下面通过分析 RIS 权重，推导出偏差的源头。这里假设所有的候选样本都来自于同一源分布 $p$ 。

4.1 分析 RIS 权重

$\eqref{1-sample RIS}$ 式的 1-sample RIS 可以重写为：
$$
\langle L\rangle^{1,M}{RIS}=f(y)\cdot\left(\frac{1}{\hat{p}(y)}\frac{1}{M}\sum\limits^M{j=1}\mathrm{w}(x_j)\right)=f(y)\mathrm{W}(\boldsymbol{x},z) \tag{9}\label{regroup 1-sample RIS}
$$
其中 $\boldsymbol{x}={x_1,x_2,\cdots,x_M}$，source PDF 的 $M$ 次独立采样；$\textup{W}$ 是 RIS 选出的样本 $y\equiv x_z$ 对应的权重，挑选过程是随机，可知是个随机变量。

理解 $y$ 与 $(\boldsymbol{x},z)$ 以及 $\textup{W}(\boldsymbol{x},z)$：首先 $(\boldsymbol{x},z)$ 表示从 $M$ 次独立采样得到的 $M$ 个样本中，随机挑选出第 $z$ 个。因此 $\boldsymbol{x}$ 是 $M$ 个独立同分布于 source PDF 的 $M$ 维随机变量，有 $p(\boldsymbol{x})=\prod\limits^M_{i=1}p_i(x_i)$；$z$ 服从一个离散分布，有 $\eqref{discrete PDF}$ 描述的条件形式。其次 $y$ 是 RIS 算法得到的样本，虽然采样过程已知，但 $y$ 的真实概率密度没有解析形式。但根据 RIS 算法，$y$ 与 $(\boldsymbol{x},z)$ 有关，但对于一个样本 $y$，会有很多种 $(\boldsymbol{x},z)$ 的组合，例如 $x_1=y$，$(x_2,\cdots,x_M)$ 随机选择，同理也可以有 $x_2=y$，因为 $\boldsymbol{x}$ 是 $M$ 次独立采样，每次采样都有可能得到样本 $y$。

对于 $\textup{W}$，虽然文中公式形式为 $\textup{W}(\boldsymbol{x},z)$，但实际意义应该是，RIS 采样得到样本 $y$ 时对应的权重，即 $x_z=y$ 的权重。换句话说，给定样本 $y$ 时的权重，权重更精确的形式是：
$$
\mathop{\textup{W}}\limits_{x_z=y}(\boldsymbol{x},z)=\frac{1}{\hat{p}(y)}\frac{1}{M}\sum\limits^M_{j=1}\textup{w}(x_j) \tag{10} \label{RIS weight}
$$
即在 $x_z=y$ 的条件下的权重。

首先猜想如何使得 RIS 估计量是个无偏估计？虽然 $y$ 的真实分布是未知的，但根据 $\eqref{IS MC}$ 式的重要性采样理论，这里的 $\textup{W}(\boldsymbol{x},z)$ 需要充当 $1/p(y)$ 的作用才能得到无偏估计，注意这里的 $p(y)$ 指的是 $y$ 的真实 PDF，而不是 source PDF，为了区分，我们重写为 $p_y(y)$。 如 $\eqref{RIS weight}$ 式描述，对于给定的 RIS 样本 $y$，可能有很多种 $(\boldsymbol{x},z)$，因此 $\textup{W}(\boldsymbol{x},z)$ 是一个随机变量，要想使得 RIS 无偏，则需要 $\textup{W}(\boldsymbol{x},z)$ 的期望值等于 $1/p_y(y)$。

[算法 4](#Algo 4) 中将多个 reservoir 整合为一个新的 reservoir 时，每个 reservoir 的权重根据 $\eqref{discrete PDF}$ 理论上应为 $\Large \frac{\hat{p}(y)}{p_y(y)}$，而算法 4 使用的近似为 $\hat{p}(y)\cdot \textup{W}$，这里则是用了 $\textup{W}$ 作为 $1/p_y(y)$ 的估计量。额外的 $M$ 则是为了对不同候选样本数量的 reservoir 进行的加权。

4.2 Biased RIS

我们将第 $i$ 次采样所服从分布的概率密度写为 $p_i(x_i)$，候选样本的联合概率密度有
$$
p(\boldsymbol{x})=\prod\limits^M_{i=1}p_i(x_i)
$$
$\eqref{discrete PDF}$ 式中候选样本的概率密度重写为
$$
p(z|\boldsymbol{x})=\frac{\textup{w}z(x_z)}{\sum^M{i=1}\textup{w}i(x_i)} \quad where \space \space \textup{w}i(x_i)=\frac{\hat{p}(x_i)}{p_i(x_i)}
$$
候选样本与选取的样本索引 $z$ 的联合概率密度为
$$
p(\boldsymbol{x},z)=p(\boldsymbol{x})\cdot p(z\mid \boldsymbol{x})=\left(\prod\limits^M{i=1}p_i(x_i)\right)\cdot \frac{\mathrm{w}z(x_z)}{\sum^M{i=1}\mathrm{w}i(x_i)} \tag{11} \label{joint PDF}
$$
对于给定样本值 $y$，可能有非常多的 $(\boldsymbol{x},z)$ 组合，对于采样出值为 $y$ 的样本 $x_i$ 要满足 $p_i(y)=p(\boldsymbol{x},i)>0$，因此所有可能情况有：
$$
Z(y)={i\mid 1\leq i\leq M \wedge p_i(y)>0 } \tag{12} \label{all z}
$$
因此最终输出 $y$ 的 PDF 可以由 $\eqref{joint PDF}$ 的联合概率密度和 $\eqref{all z}$ 的所有可能取值得到
$$
p_y(y)=\sum\limits{i\in Z(y)}\underbrace{\int\cdots\int}{M-1} p(\boldsymbol{x}^{i\rightarrow y},i) \space \underbrace{dx_1\cdots dx_M}{M-1} \tag{13} \label{y PDF}
$$
$p(\boldsymbol{x}^{i\rightarrow y},i) $ 是参照 $\eqref{joint PDF}$ 代入 $z=i,x_i=y$ 得到的 $(x_1,\cdots,x{i-1},y,x_{i+1},\cdots,x_M)$ 的联合概率密度，对每种可能取值下的联合概率密度求 $y$ 的边缘概率密度 $p_i(y)$，并求和得到 $p_y(y)$。

验证 RIS 是否无偏，需要知道 $\eqref{RIS weight}$ 中描述的权重的期望是否为 $1/p_y(y)$，求解其期望如下：
$$
\mathop{\mathbb{E}}\limits_{x_z=y}\left[\textup{W}(\boldsymbol{x},z)\right]=\frac{1}{p_y(y)}\frac{|Z(y)|}{M} \tag{14} \label{weight expectation}
$$
由 $\eqref{all z}$ 可知，只有在所有候选样本分布都不为 0 时，上式的权重期望才为 $1/p_y(y)$，RIS 才是无偏的。

如果部分积分区域上的 source PDF 为 0，则有 $\large\frac{|Z(y)|}{M} < 1$， 此时，重要性采样的 inverse PDF 会偏小，积分结果会偏小，带来能量损失。

4.3 Unbiased RIS

上一节给出了 RIS 有偏的情况，即会有部分样本的 source PDF 为 0。这是由于 visibility 项导致的，我们在复用其他像素的 reservoir 时，并没有考虑这些 reservoir 样本是否对当前像素可见。同样，在执行 [算法 3](#Algo 3) streaming RIS 时，会根据 shadow ray 丢弃掉部分不可见候选样本，但在复用阶段，这些被丢弃的样本可能对当前像素是可见的，这就损失了部分能量。

因此若想得到无偏 RIS 则需要对 $\eqref{RIS weight}$ 和 $\eqref{weight expectation}$ 的候选样本的总数 $M$ 进行调整，调整为当前像素可见的候选样本总数，设置 $m(x_z)=\frac{1}{M}$，新的权重及其期望形式为
$$
\begin{align}
\mathop{\textup{W}}\limits_{x_z=y}(\boldsymbol{x},z)&=\frac{1}{\hat{p}(x_z)}\left[m(x_z)\sum\limits^M_{j=1}\textup{w}(x_j)\right] \
\mathop{\mathbb{E}}\limits_{x_z=y}\left[\textup{W}(\boldsymbol{x},z)\right]&=\frac{1}{p_y(y)}\sum\limits_{i\in Z(y)}m(x_z)
\end{align}
$$
因此当 $\sum\limits_{i\in Z(y)}m(x_z)=1$ 时，RIS 为无偏估计。如何保证这一条件？

4.4 A Practical Algorithm for Unbiased Reuse

本文使用光源分布作为 source PDF，候选样本以及选出的 reservoir 样本都是光源面上一点。并且对于直接光照采样，只会采样着色点可见光源，即 $\eqref{weight expectation}$ 中使用的候选样本分布都不为 0，因此对于初始候选样本重采样的过程是无偏的。但对于reservoir 重用过程，新的 reservoir 的 source PDF 变成了，每个 reservoir 样本的分布，这个是未知的，因此重用过程的 source PDF 可能互不相同。重用过程引入 bias 的原因是：尽管复用 reservoir 对其像素可见，但对于当前像素可能不可见，这就导致了新 reservoir 的部分 source PDF 为 0，为 $\eqref{weight expectation}$ 引入了 bias。

论文中提出一种无偏 RIS 算法，该算法基于一种观察：尽管复用 reservoir 样本 PDF (即新 reservoir 的 source PDF)不可知，但当样本对当前像素不可见时，其 PDF 为 0。因此可以在复用 reservoir 样本之前，先进行 visibility 测试，如果不可见，设置其 PDF 为 0，即丢弃掉该样本，也就是 visibility reuse。相比有偏算法，无偏算法开销很大，因为需要对每个复用 reservoir 样本发射一条 shadow ray。

5 Design and Implementation

作者为有偏与无偏算法选用不同的参数配置，以达到两种算法的开销近似。

$M=32$ 个初始候选样本的生成：根据三角面片发光的 power 重要性采样选择一个三角形，然后在三角形上均匀采样一个点 $x$，即 source PDF $p(X)\propto L_e(x)$。如果有环境光贴图，那么 25% 的候选样本由重要性采样环境光贴图生成。重要性采样发光三角形与环境光贴图都是离散采样，采用 alias table [2]。同时，作者也测试了通过预计算为场景的发光三角形生成 VPL 集合，虽然能够提高性能，但有 visual artifact。

Target PDF：在重采样步骤中，需要 target PDF 对选出的样本进行加权，作者使用 unshadowed path contribution 作为 target PDF，即 $\hat{p}\propto \rho\cdot L_e\cdot G$。作者为场景所有几何使用统一的材质，Lambertian diffuse 和 dielectric GGX microfacet 。而对于复杂的材质模型，为每个候选样本计算会更耗时。

Neighbor Selection：对于 Spatial Reuse，在 30-pixel 半径范围内采样 $k$ 个像素进行复用，无偏选用 $k=3$，有偏选用 $k=5$。对于 Temporal Reuse，则使用 motion vector 找到历史帧对应的像素。

Biased RIS 降低偏差：对于有偏算法，重用来自不同几何/材质的像素会增加偏差，因此作者使用一种简单的启发式策略拒绝这部分像素。比较重用像素与当前像素的到相机距离、normal 夹角，拒绝超过预设阈值的像素(10% 当前像素的深度和 25°)。

Evaluated Sample Count：对于 [算法 5](#Algo 5) ，每个像素存储 $N$ 个 reservoir，无偏算法采用 $N=1$，有偏算法采用 $N=4$。

Reservoir storage and temporal weighting：每个像素只存储选出的样本 $y$ 及其权重 $W$，候选样本的数量 $M$。对于 temporal reuse，对当前像素产生贡献的候选样本数量会无限制增加，因为每一帧都结合了历史帧的 reservoir。在重采样过程中，这样会导致 temporal sample 加权高度不成比例，作者将历史帧的候选样本数量限制在当前帧 $20\times M$ 内，这样就限制了时序信息的影响。

Reference

[1] Benedikt Bitterli, Chris Wyman, Matt Pharr, Peter Shirley, Aaron Lefohn, and Wojciech Jarosz. 2020. Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting. ACM Trans. Graph. 39, 4, Article 148 (August 2020), 17 pages.

[2] Alastair J Walker. 1974. New fast method for generating discrete random numbers with arbitrary frequency distributions. Electronics Letters 10, 8 (1974), 127–128.

[3] Justin F. Talbot. 2005. Importance Resampling for Global Illumination. Masters Thesis. Brigham Young University

Appendix

1. 重要性采样为何要到 Resample Importance Sampling

蒙特卡洛积分估计理论上是进行越多的采样次数，越接近 ground-truth，但实际中要限制开销，只能以有限的采样次数来进行积分估计。因此，采样分布如果能够更倾向于采样被积函数较重要的区域，则会更快达到收敛，这就是重要性采样 (IS) 的思想。$\eqref{IS MC}$ 式描述的重要性采样(IS)是蒙特卡洛积分的最简单的无偏估计，因为 IS 只采样了一种分布，例如 cosine-weighted sample hemisphere 就是根据渲染方程 cosine 项的特征得到的采样方法。

但通常渲染方程被积函数包含多项，如 $\eqref{simple render equation}$ 中的 $\rho,L_e,G$ 等。于是又有了，$\eqref{MIS MC}$ 式描述的多重重要性采样，MIS 使用了多种采样策略，每种采样策略都进行了一次重要性采样，最后将多次重要性采样结合在一起。虽说，MIS 考虑了多种分布，但其估计量形式相当于是对多种分布的线性组合，而对于渲染方程而言，其被积函数是多项的乘积形式，因此不能更好地采样被积函数的重要性区域。

对于多种分布的乘积形式，是无法直接采样的。但可以使用 Resample Importance Sampling(RIS) $\eqref{1-sample RIS}$ 来近似成比例地采样多种分布乘积形式。

2. RIS 权重期望

$$
\begin{align}
\mathop{\mathbb{E}}\limits_{x_z=y}\left[\textup{W}(\boldsymbol{x},z)\right]&=\underbrace{\int \cdots \int}M\frac{ \textup{W}(\boldsymbol{x},z,x_z=y)\cdot p(\boldsymbol{x},z,x_z=y)}{p_z(x_z=y) \space } \space dx_1\cdots dx_Mdz \
&\overset{\eqref{y PDF}}{=}\sum\limits{i\in Z(y)}\underbrace{\int\cdots\int}{M-1} \frac{ \textup{W}(\boldsymbol{x}^{i\rightarrow y},i)\cdot p(\boldsymbol{x}^{i\rightarrow y},i)}{p_y(y) } \space dx_1\cdots dx_M \
&= \sum\limits{i\in Z(y)} \frac{\underbrace{\int\cdots\int}{M-1} \textup{W}(\boldsymbol{x}^{i\rightarrow y},i)\cdot p(\boldsymbol{x}^{i\rightarrow y},i)\space dx_1\cdots dx_M}{p_y(y)} \
&= \frac{1}{p_y(y)}\cdot \sum\limits{i\in Z(y)} \underbrace{\int\cdots\int}{M-1} \textup{W}(\boldsymbol{x}^{i\rightarrow y},i)\cdot p(\boldsymbol{x}^{i\rightarrow y},i)\space dx_1\cdots dx_M \
&\overset{代入 \eqref{RIS weight},\eqref{joint PDF}}{=} \frac{1}{p_y(y)}\sum\limits{i\in Z(y)}\int\cdots\int \left(\frac{1}{\hat{p}(x_i)}\frac{1}{M}\sum\limits^M_{j=1}\textup{w}(x_j)\right) \left(\prod\limits^M_{j=1}p_j(x_j)\right) \frac{\textup{w}i(x_i)}{\sum^M{j=1}\textup{w}j(x_j)} \space dx_1\cdots dx_M \
&= \frac{1}{p_y(y)}\sum\limits{i\in Z(y)}\int\cdots\int \left(\frac{1}{\hat{p}(x_i)}\frac{1}{M}\right) \left(\prod\limits^M_{j=1}p_j(x_j)\right) \textup{w}i(x_i) \space dx_1\cdots dx_M \
&= \frac{1}{p_y(y)}\sum\limits{i\in Z(y)}\left(\frac{p_i(x_i)}{\hat{p}(x_i)}\frac{\textup{w}i(x_i)}{M}\underbrace{\int\cdots\int \prod\limits^M{j\neq i}p_j(x_j) \space dx_1\cdots dx_M}1\right) \
&=\frac{1}{p_y(y)}\sum\limits{i\in Z(y)}\left(\frac{p_i(x_i)}{\hat{p}(x_i)}\frac{\textup{w}i(x_i)}{M}\right) \
&= \frac{1}{p_y(y)}\sum\limits{i\in Z(y)}\frac{1}{M} \
&= \frac{1}{p_y(y)}\frac{|Z(y)|}{M}
\end{align}
$$

Paper Notes > Ray Tracing
Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting
http://example.com/2023/09/20/Paper Notes/Ray Tracing/Spatiotemporal reservoir resampling for real-time ray tracing with dynamic direct lighting/
Author
John Doe
Posted on
September 20, 2023
Licensed under