Basic Radiometry

辐射度量学基础

Whitted style 光线追踪使用 Blinn-Phong 着色模型，着色效果不真实。因此有提出基于辐射度量学的着色模型，以物理正确的方式进行光照计算。

相关术语

物理量	公式	单位
Radiant Energy(辐射能)	$Q=\frac{hc}{\lambda}$	$J$(焦耳)
Radiant Flux(辐射通量)或Power(功率)	$\Phi=\frac{dQ}{dt}$	$W$(瓦特) 或 lm
Angle(角度)	$\theta=\frac{l}{r}$	rad(弧度)
Solid Angle(立体角)	$\Omega=\frac{A}{r^2}$	sr(球面角度)
Radiant Intensity(辐射强度)	$I=\frac{\Phi}{4\pi}$	$W/sr$ 或 cd(烛光)
Irradiance(辐照度)	$E(x)=\frac{d\Phi (x)}{dA}$	$W/m^2$ 或 lux(照度)
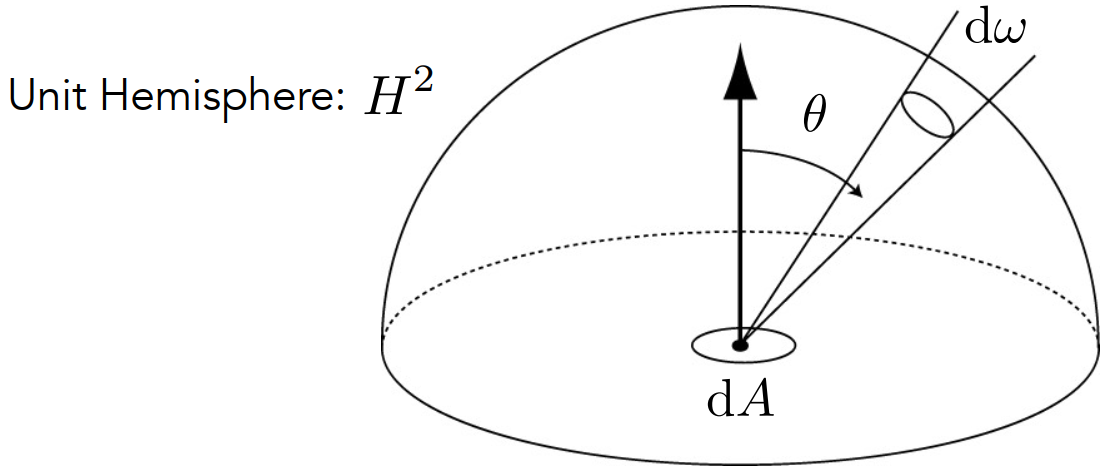
Radiance(辐射率)或luminance(亮度)	$L(p,\omega)=\frac{d^2\Phi (p,\omega)}{d\omega dA cos\theta}$	$W/(m^2\cdot sr)$ 或 nit(尼特)

1. Radiant Energy(辐射能量)

电磁辐射的能量，单位焦耳 $J$

光源发射光子，每个光子具有特定的波长以及特定数量的能量。波长为 $\lambda$ 的光子携带的能量
$$
Q = \frac{hc}{\lambda}
$$
其中，$c$ 为光速，$h$ 为普朗克常量

2. Radiant Flux/Power(辐射通量/功率)

单位时间内通过表面或空间区域的能量，即功率

$$
\Phi = \frac{dQ}{dt}
$$

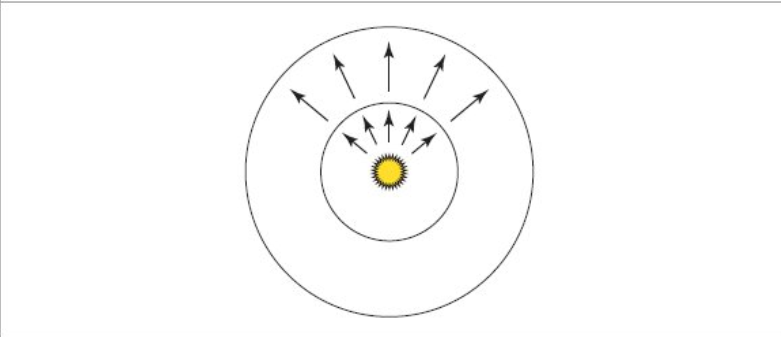
光源发出(emitted)的总量通常使用通量描述。下图描述了来自点光源的通量通过球面的能量，在两个球上测量得到的通量应该是相同的。

经常会遇到throughput说法，但throughput并不是物理量，只是对光线传播时所保持能量的描述。例如由光源发出的光线，经过一级反射会累积交点处的BSDF，在下一级光路传播时，该光线的throughput指的是其携带能量乘上BSDF。可以理解为 scaled radiance。而辐射通量则是某点对到达该点的光线的throughput * 该点的BSDF的积分。

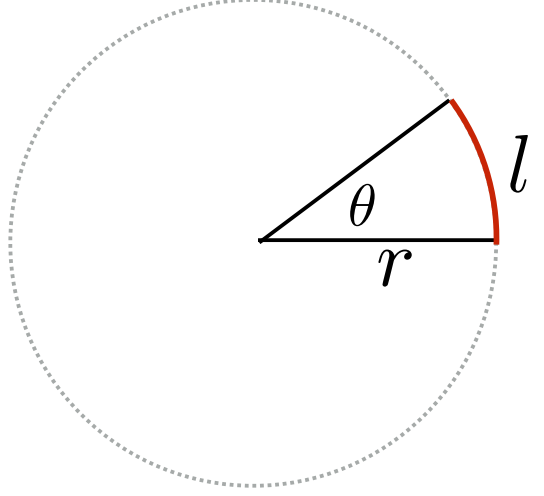
3. Angle

圆上的弧长与半径的比值: $\theta=\frac{l}{r}$ ，圆有 $2\pi$ 弧度

4. Solid Angle(立体角)

球面上的投影面积与半径的平方之比: $\Omega = \frac{A}{r^2}$，球的立体角为 $4\pi$ 球面角度(steradians)

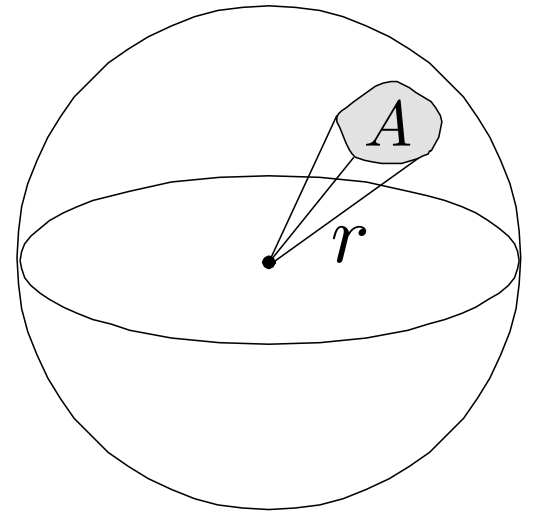
5. Differential Solid Angle(微分立体角)

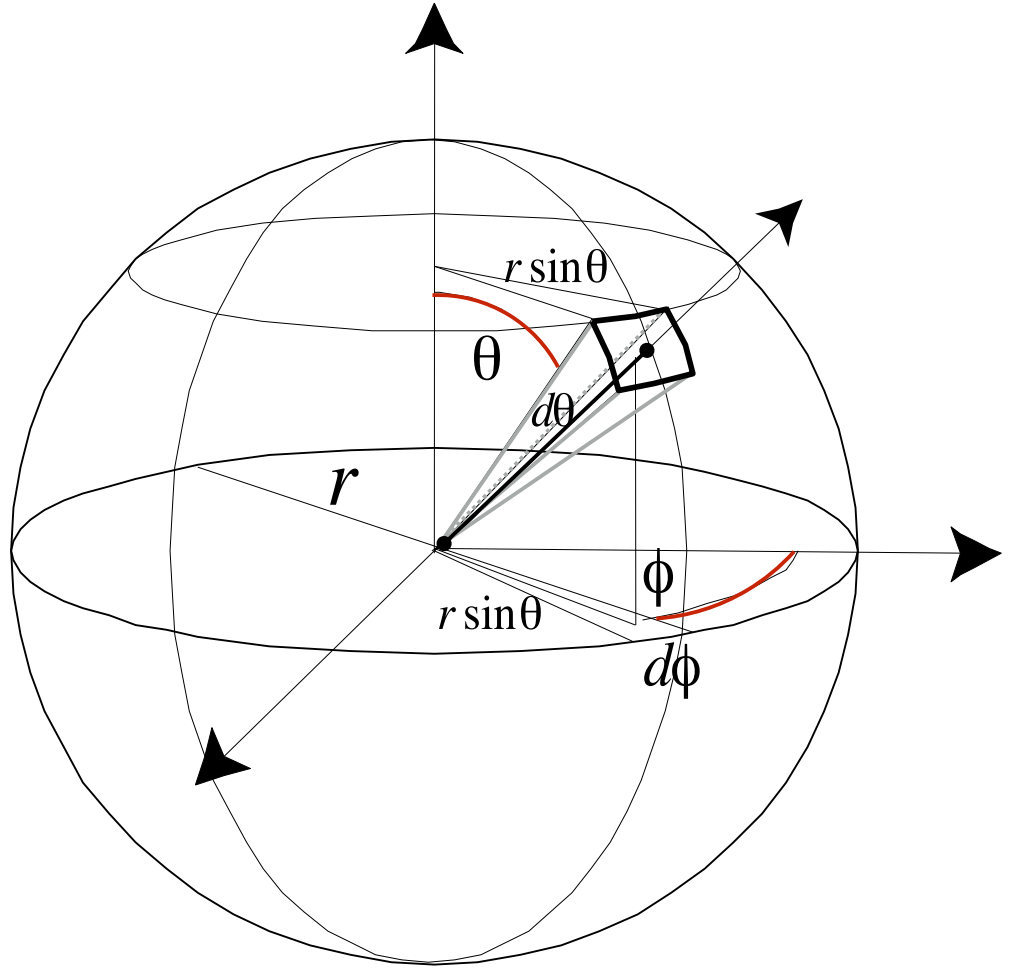
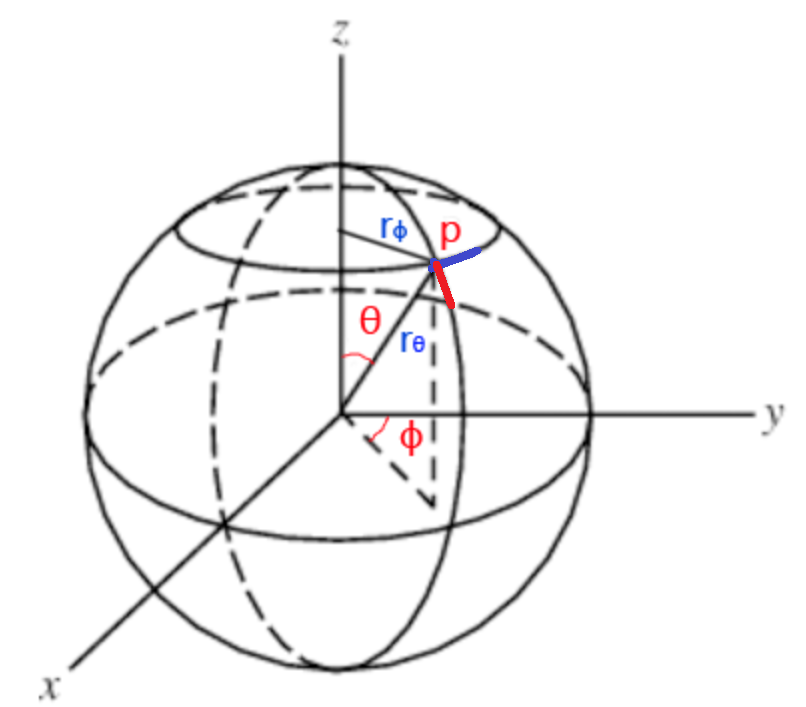
球面坐标：$\theta\in[0,\pi],\phi\in[0,2\pi]$
单位面积：$dA=(rd\theta)(rsin\theta d\phi)=r^2sin\theta d\theta d\phi$，单位立体角对应的球面上单位区域的面积
单位立体角：$d\omega = \frac{dA}{r^2}=sin\theta d\theta d\phi$
球面的微分立体角：$\Omega=\int_{S^2}d\omega=\int_0^{2\pi}\int_0^{\pi}sin\theta d\theta d\phi=4\pi$，其中 $S^2$ 是球面积

$dA$ 的证明，$dA$ 可看作 $d\theta$ 和 $d\phi$ 对应的微分弧组成的小矩形，如下图中红色弧线与蓝色弧线

其中蓝色弧线位于半径为 $r_\phi$ 的小圆上，而红色弧线位于半径为 $r_\theta$ 的大圆上，又知道 $sin\theta = \frac{r_\phi}{r_\theta}$，由弧长公式有

红色弧：$r_\theta d\theta$，蓝色弧：$r_\phi d\phi=r_\theta sin\theta d\phi$。

因此 $dA=(r_\theta d\theta)(r_\theta sin\theta d\phi)=r_\theta^2sin\theta d\theta d\phi$。

$sin\theta$ 的直观理解是，越靠近极点位置，$r_\phi$ 越小，因此微分面积也越小；越靠近赤道位置，$r_\phi$ 越大，因此微分面积也越大

$\omega$ 作为单位立体角的方向向量

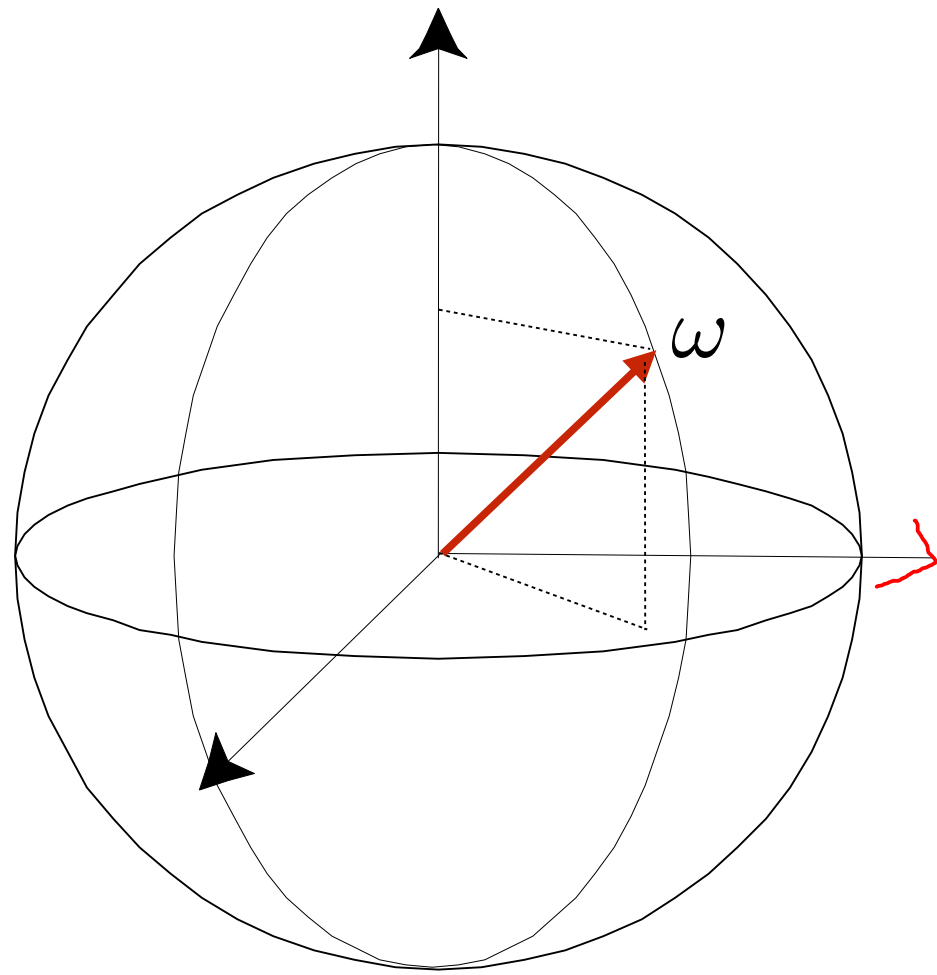
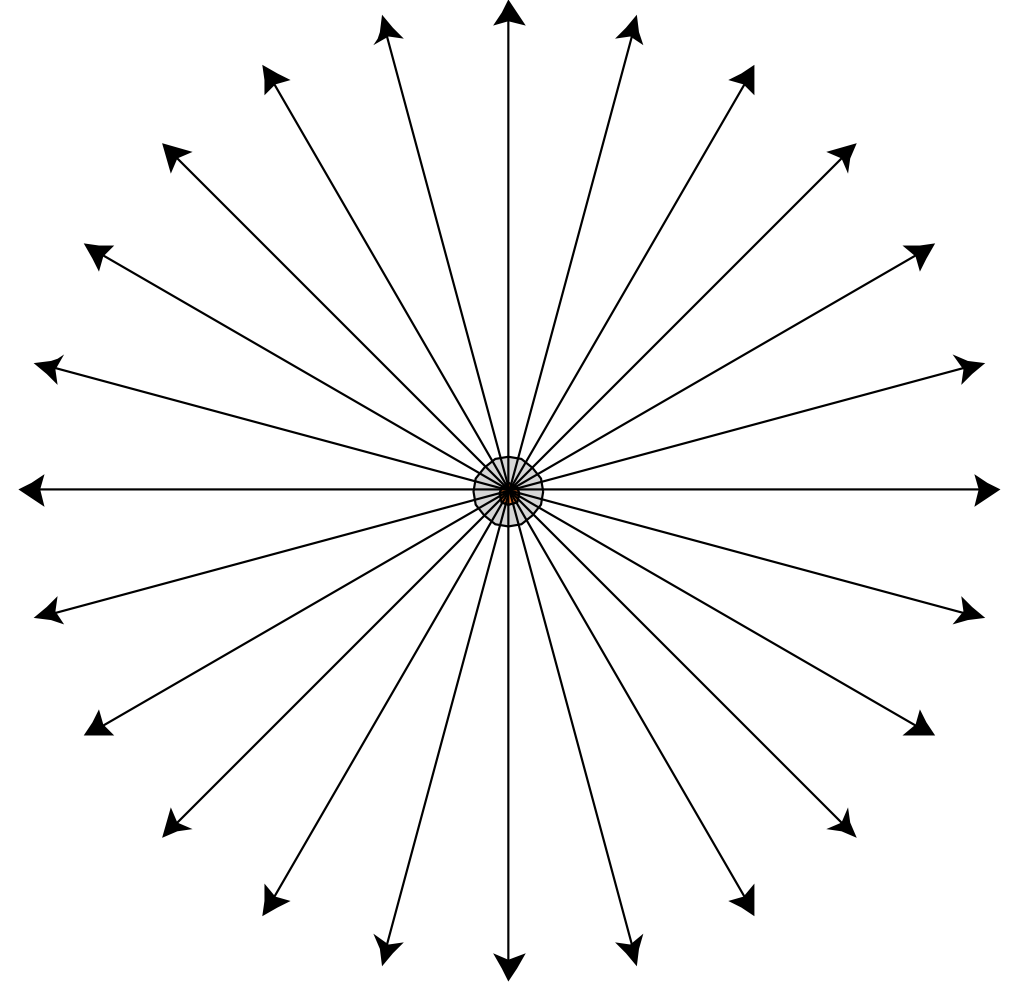
Isotropic Point Source(各向同性光源)：球面上各单位立体角辐射强度 (Radiant Intensity) 相同。整个球面的辐射通量/功率：$\Phi=\int_{S^2}Id\omega=4\pi I$，辐射强度 $I=\frac{\phi}{4\pi}$。

6. Radiant Intensity(辐射强度)

点光源每立体角发出的功率
$$
I(\omega)=\frac{d\Phi}{d\omega}
$$

7. Irradiance(辐照度)

前述flux(辐射通量或功率)是单位时间内通过表面的能量，irradiance则为辐射通量在表面上的平均强度，即单位面积的强度。

辐照度是每(垂直/投影)单位面积入射到一个表面上一点的辐射通量(功率)，
$$
E(x)=\frac{d\Phi(x)}{dA}
$$

单位时间内光子离开或进入单位面积的通量

Lambert 余弦定律：表面辐照度与光方向和表面法线夹角的余弦值成正比

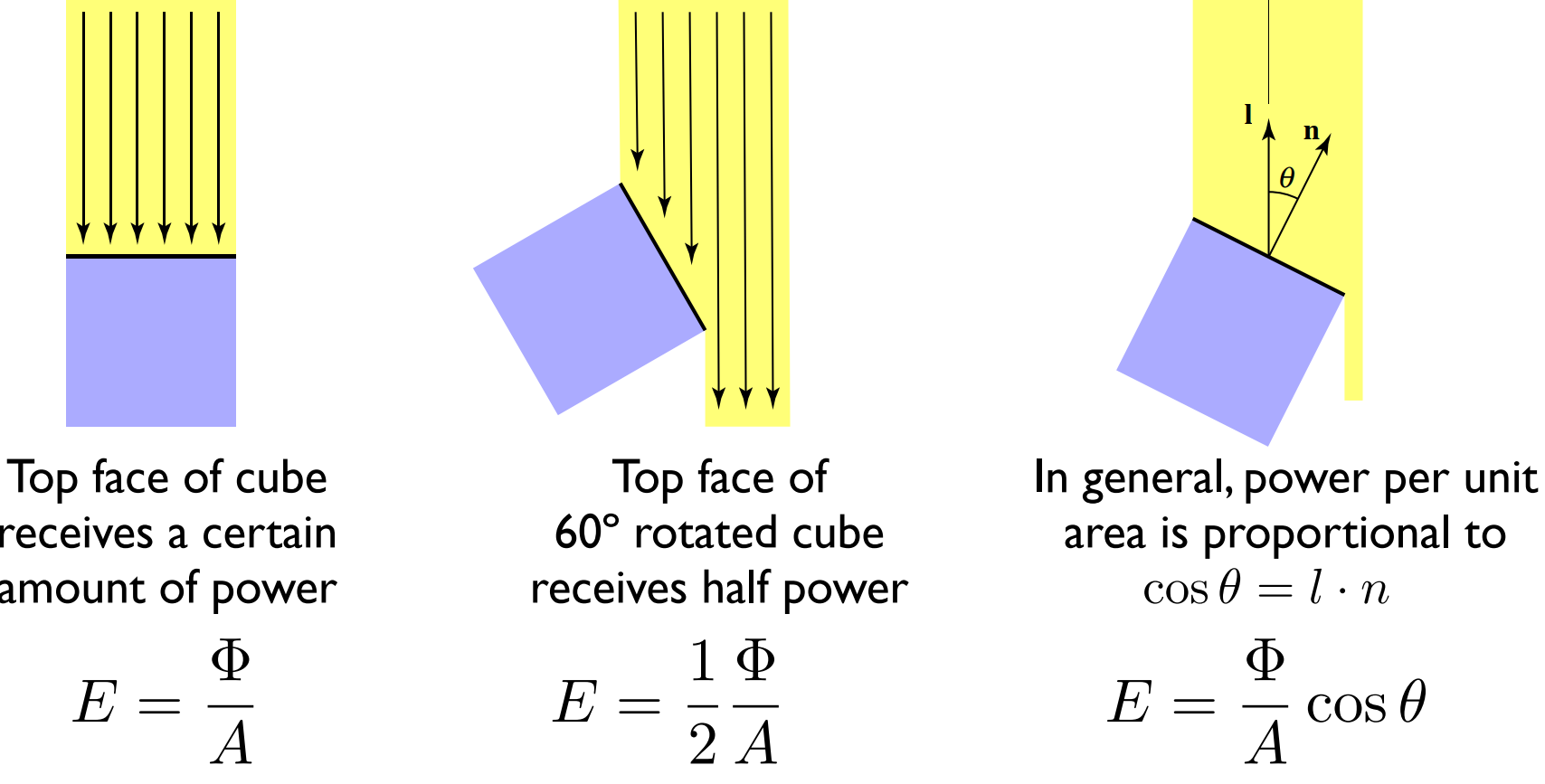
这里 irradiance 是单位面积入射到一点的辐射通量，$cos\theta$ 调整的是方向 $l$ 上入射功率的贡献，将方向 $l$ 上的辐射通量投影到接收点的法线方向 $n$ 上。

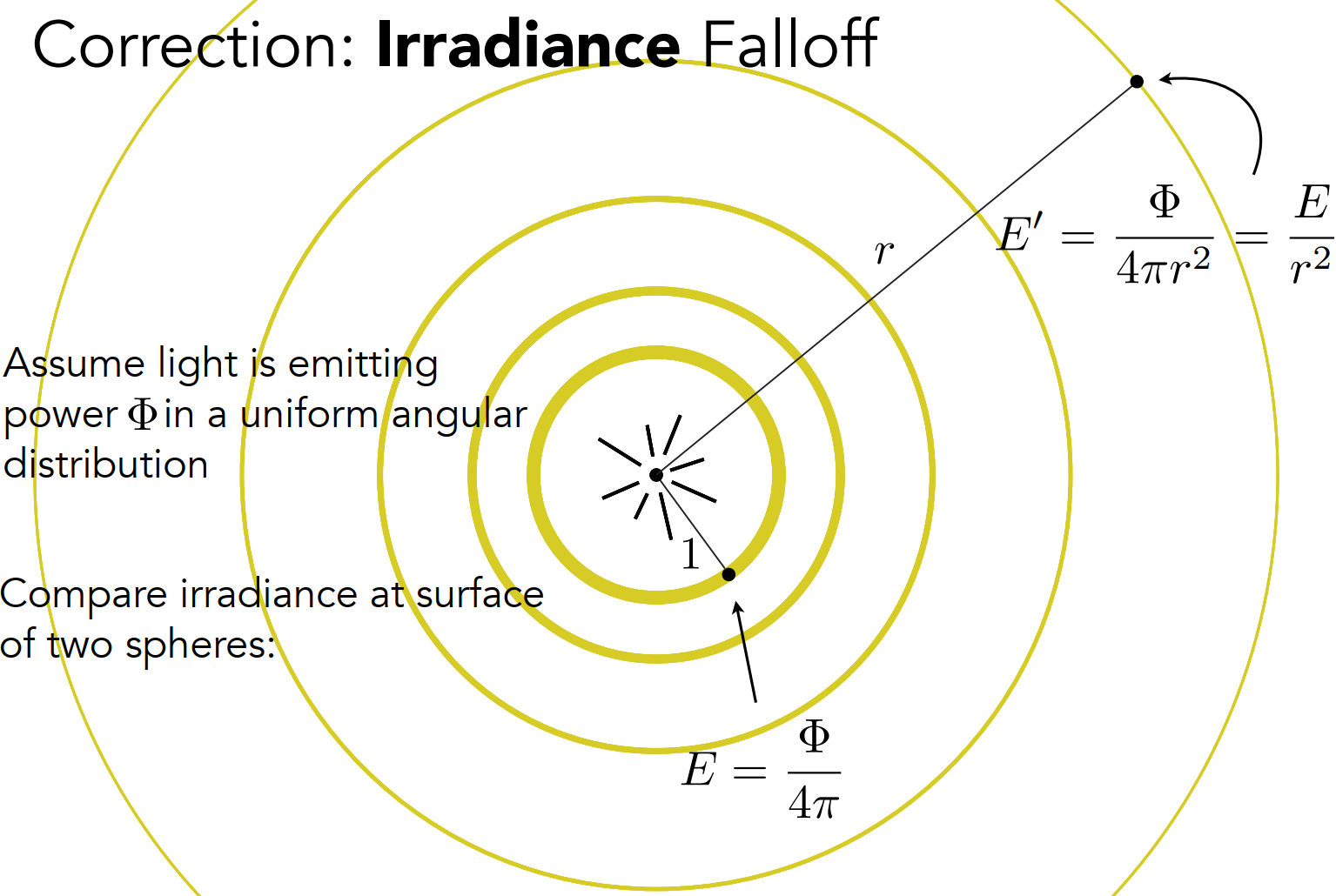
Irradiance 衰减：$E=\frac{\Phi}{4\pi r^2}$ ，$\Phi$ 记录的是单位半径球面在单位时间内所接收的能量的功率。二维示意图如下

8. Radiance(辐射率)

Radiance 用于描述光在环境中的分布的基本场量。辐射率(Radiance)或亮度(luminance) ：是指一个表面在每单位立体角、每单位投影面积上所发射(emitted)、反射(reflected)、透射(transmitted)或接收(received)的辐射通量(功率)。

$$
L(p,\omega)=\frac{d^2\Phi (p,\omega)}{d\omega dA \cos\theta}
$$

$p$ 点所在表面、立体角方向$w$接收到的辐射通量 $\Phi(p,w)$，对立体角、面积的二阶求偏导的辐射率 $L(p,w)$。反过来求辐射通量，这里得到的是表面的整个积分域与立体角的积分域收到的辐射通量。
$$
\Phi(p,w)=\int\int L(p,w)\cdot \cos\theta\space dwdA
$$

Light traveling along a Ray