Massively Parallel Path Space Filtering
1 Summary
2 Background
计算 $x$ 点处在 $\omega_r$ 方向上反射的 radiance $L_r$ 有如下四种方式:
$$
\begin{align}
&L_r(x, \omega_r) \
&= \int_{S^2}L_i(x, \omega)f_r(\omega_r, x, \omega) \cos\theta_x \space d\omega \tag{1}\
&= \int_{\partial V}V(x,y) L_i(x, \omega)f_r(\omega_r, x, \omega)\cos\theta_x\frac{\cos\theta_y}{|x-y|^2}\space dy \tag{2}\
&= \lim_{r(x)\rightarrow 0}\int_{\partial V} \int_{S^2(y)}\frac{\mathcal{X_B}\left(x-h(y,\omega), r(x)\right)}{\pi r(x)^2}L_i(h(y,\omega),\omega)\cdot f_r(\omega_r,h(y,\omega), \omega)\cos\theta_y\space d\omega dy \tag{3}\
&= \lim_{r(x)\rightarrow 0}\int_{S^2}\frac{\int_{\partial V}\mathcal{X_B}(x-x’,r(x))\mathrm{w}(x,x’)L_i(x’,\omega)f_r(\omega_r,x,\omega)\cos\theta_{x’}\space dx’}{\int_{\partial V}\mathcal{X}_B(x-x’,r(x))\mathrm{w}(x,x’)\space dx’}\space d\omega \tag{4}
\end{align}
$$
其中 $\mathcal{X}_B$ 是特征函数(又称指示函数),点 $x$ 到球心 $c$ 距离为 $d=||c-x||_2$,球半径为 $r$,有 $\mathcal{X_B}(d, r) = \begin{cases} 1 \quad d^2 < r^2 \ 0 \quad otherwise \end{cases}$ 。 上面描述了不同的技术:
- (1):基础的forward path tracing下的反射项计算,对着色点处法线方向的半球面的积分。
- (2):Next Event Estimation and Subpath Connection,将 (1) 的积分域转换到场景中的表面上,采样表面上一点,与该点或者该点的路径进行连接。
- (3):Density Estimation,photon mapping理论。使用特征函数将 density estimation 区域限制在着色点附近以 $r(x)$ 为半径的球内,density通过除以着色点所在平面与球相交部分的面积得到。
- (4):Path Space Filtering,与photon mapping的density estimation 不同,path space filtering在球内计算采样点相对于着色点的权重,进行加权平均。
下图展示了不同技术的过程,
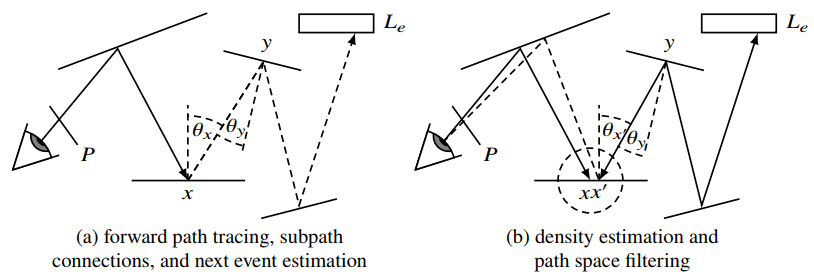
path space filter 原理如下
$$
\bar{c_i} = \frac{\sum_{j=0}^{b^m-1} \mathcal{X}{\mathcal{B}(n)}(x{s_i+j} - x_i) \cdot w_{i,j} \cdot c_{s_i+j}}{\sum_{j=0}^{b^m-1} \mathcal{X}{\mathcal{B}(n)}(x{s_i+j} - x_i)\cdot w_{i,j}} \label{path-filter} \tag{5}
$$
3 Algorithm
与 [2] 中类似,算法输入为一组顶点,这些radiance信息要被filtered。除此之外,在一个hash table中存储与查找。
3.1 Averaging in Voxels
与 $\eqref{path-filter}$ 中特征函数基于三维球不同,本文提出的算法使用从顶点描述中构建得到 key k。
3.1.1 Characteristic Function of a Voxel
给定一个resolution selection函数 $s(k)$,voxel的特征函数定义为
$$
\mathcal{X}_V(k,k’) =
\begin{cases}
1 \quad \lfloor s(k)k\rfloor=\lfloor s(k’)k’\rfloor \wedge s(k)=s(k’) \
0 \quad \mathrm{otherwise}
\end{cases}
\label{characteristic-function}\tag{6}
$$
s(k) 可以理解为是一个基于key k的投影过程,将 k 投影到一个voxel中
- $s(k)k$ 向下取整,意味着 $s(k)$ 表示 1.0 / resolution。第一项表示 k、k’ 所属 voxel 相同
- $s(k)=s(k’)$ ,表示所选resolution相同,即二者位于同一voxel层级
这两个条件确定二者属于同一个voxel。
$s(k)$ 可以选择常量,即所有voxel具有相同的大小;更明智的,随着距离相机越远,voxel范围随之增大,这意味着距离远的voxel会更激进地filter以及具有更低密度的路径顶点。作者选择通过计算一块区域在屏幕上的投影大小来实现 $s(k)$ 的参数化。实现如 [算法1](#Algorithm 1) ,会先根据顶点到相机的距离计算一个层级,不同层级具有不同的分辨率。
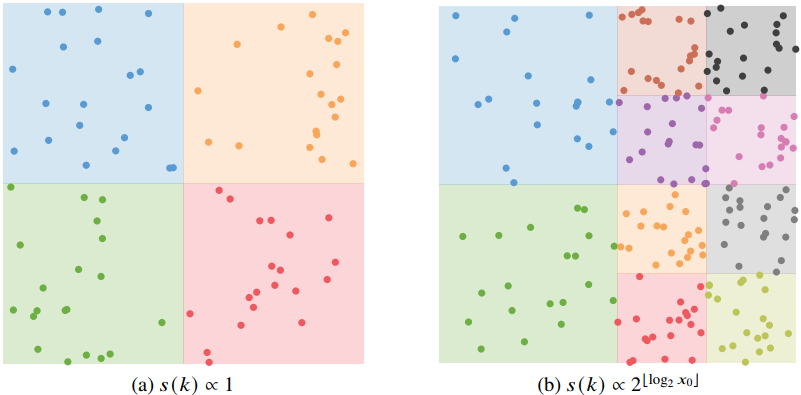
使用 $\mathcal{X}V$ 替换 $\eqref{path-filter}$ 的特征函数,以及设置权重为1,得到
$$
L_r(x,\omega_r) \approx \int{S^2}\frac{\int_{\partial V}\mathcal{X}V(k,k’)L_i(x’,\omega)f_r(\omega_r,x,\omega)\cos\theta{x’}\space dx’}{\int_{\partial V}\mathcal{X}V(k,k’)\space dx’}d\omega
$$
上述积分项依赖于着色点,因此每次着色一个点时都需要计算一次。接下来,简化该积分,剥离着色点。将 $f_r(\omega_r,x,\omega)\approx f_r(\omega_r,x)\cdot f_i(x,\omega)$,$f_i(x,\omega)$ 在voxel近似为常量,因此可以得到
$$
L_r(x,\omega_r) \approx f_r(\omega_r,x)\cdot \int{S^2}\frac{\int_{\partial V}\mathcal{X}V(k,k’)L_i(x’,\omega)f_i(x’,\omega)\cos\theta{x’}\space dx’}{\int_{\partial V}\mathcal{X}_V(k,k’)\space dx’}d\omega \label{voxel-filter} \tag{7}
$$
此时,积分项中还有隐藏的着色点,$k$ 是由着色点信息构建的,但 $\mathcal{X}_V(k,k’)$ 对于具有 key k 的所有顶点都是相同的,因此积分项只与voxel中的顶点相关,每个voxel只需要计算一次该积分。
3.1.2 Construction of Keys
key $k$ 只会包含描述中的一部分组件,$\eqref{voxel-filter}$ 式中积分只与 key 中包含的部分有关。key包含哪些components是bias与方差之间的权衡:
- 包含更多components,可能会减少bias,但会导致方差增大
- 包含更少components,可能会减小方差,但会导致bias增加
$\eqref{voxel-filter}$ 式中的近似很大程度取决于 $L_i$ 在 $x’$ 与 $x$ 之间的偏差。
- 首先最重要的是限制voxel在世界空间的范围,这通过在 key 中包含顶点坐标实现。然而实际中,$L_i$ 不是连续的,例如锐利阴影边缘。近似带来的视觉误差会随着voxel减小而减小。
- 另一点 $\lim_{x’\rightarrow x}\cos\theta_{x’}=\cos\theta_x$ 也无法得到保证,也就是表面朝向不连续,例如,物体的锐利边缘。因此在key中包含顶点法线可以避免抹除或平坦边缘。
- 将 $f_r(\omega_r,x,\omega)$ 拆分为 $f_r(\omega_r,x)\cdot f_i(x,\omega)$ 对于高反射的镜面是不可行的。但在glossy表面,filtering可以以一定偏差高效降低方差。对于这类表面,拆分入射角,为每个拆分区间计算平均值可能是个可行的折衷方案。因此将入射角度包含到key中。
- 材质通常由多个具有不同属性的layers组成。独立地filter这些layers可以做到为不同layers的key选择不同的components,以及不同的resolutions。例如,一个material包含一个在diffuse layer之上的glossy layer,仅需要在glossy layer的filter中包含 $\omega_r$,因为diffuse layer与观察角度无关。而diffuse layer也可以包含更多样本。在key中增加一个layer的标记,将平均值分割成几个单独的部分,并在之后组合起来。
这些key的组成部分在经过 $\eqref{characteristic-function}$ 的量化,会按照各组成部分划分区域,例如 position 组成部分划分世界空间、入射角度划分入射区域。
3.1.3 Adaptive Resolution
分辨率选择函数 $s(k)$ 对于找到视觉偏差与方差之间的权衡非常重要。理论上,$s(k)$ 在具有高频细节 $L_i$ 的区域应该更大(1.0 / resolution),但这样的信息是未知的。下图展示了,硬阴影由于filter而模糊,

空间差异可用于适应性启发式算法,但需要引入一定的计算开销。具体如何,论文中没有提及。
3.1.4 Filter Kernel Approximation by Jittering
抖动key的组成部分可以消除 $s(k)$ 量化过程的不连续性。如何抖动取决于 key 组成部分的种类,例如顶点坐标选择在切平面抖动。
经过抖动产生的噪声明显由于量化产生的离散化伪影,且更容易被filter,如下图

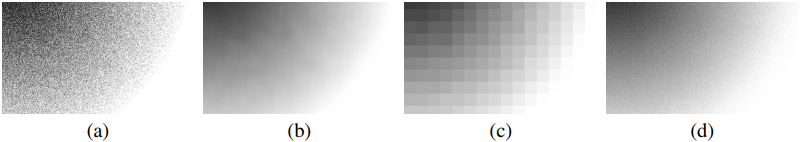
3.2 Accumulation and Lookup in a Hash Table
计算 voxel 的积分项有两种方式:
- 为每个voxel遍历其包含的顶点,这种方式需要维护voxel的顶点列表
- 直接遍历所有顶点,将顶点的贡献 $L_i(x’,\omega)f_i(x’,\omega)\cos\theta_{x’}$ 以原子操作累积到对应voxel上,并进行计数,这种方式无需维护列表。
对于现代GPU,第二种方式更加高效,但需要一个顶点 key 到 voxel 的映射,这是通过一个hash table完成的。首先使用一个 fast hash function 计算key的hash,并使用取模运算 % 映射到 table cells 索引范围内。为了解决碰撞,还需要在hash table中存储key,在得到索引后,比较对应key。当不同key映射到同一index时,使用 linear probing,增加index继续搜索。
3.2.1 Fingerprinting
key中包含了多个组成部分,因此比较完整的key是比较耗费性能的。作者选择再使用一个 hash,得到hash值作为 fingerprinting,来标记唯一的entry。fingerprinting也会小概率碰撞,但作者以小概率错误的代价换取性能提升,因为原key的比较非常耗费性能。过程如 [算法1](#Algorithm 1) 所示

3.2.2 Searching by Linear Probing
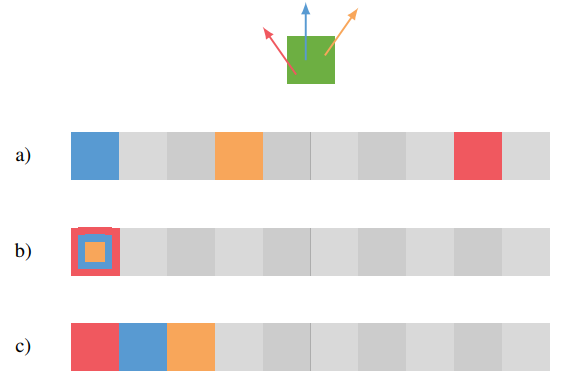
如 [算法1](#Algorithm 1) 中所示,先将顶点坐标变换到voxel坐标 $\bar{x}$ ,后续的hash操作都是针对voxel坐标进行的。线性探测过程可用于在更精细分辨率下区分光路的属性。如下图所示:
- (a):将normal直接包含在main key中,即第一次hash过程。位于同一voxel的三个顶点由于normal不同,经过hash,落在了不同的cell。
- (b):如果main key中不包含normal,同一voxel的顶点落在同一cell中
- (c):normal加入第二次hash,得到的fingerprint可以区分normal的不同。线性探测的查找过程即可遍历这些位于同一voxel但不同normal的顶点。
3.3 Handling Voxels with a low Number of Vertices
对于只有少量顶点的voxel,上述variance reduction是较差的。
3.3.1 Neighborhood Search
voxel的累积过程需要对每个顶点的radiance的每个组成部分执行一次 atomicAdd,最终的均值只需要 non-atomic 读取每个component,求和并除以 counter。因此,只要访问hash table是常量时间,那么均值计算也是常量时间。
有两种方式,邻域搜索或者在更粗粒度层级的voxel中。邻域搜索需要多次查找hash table,而后者则只需要一次查找。
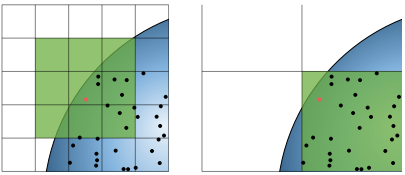
3.3.2 Multi-level Accumulation
3.4 Accumulation Over Time
Reference
[1] Binder, N., Fricke, S., and Keller, A. 2021. Massively Parallel Path Space Filtering.
[2] Alexander Keller, Ken Dahm, and Nikolaus Binder. 2016. Path space filtering. In Monte Carlo and Quasi-Monte Carlo Methods: MCQMC, Leuven, Belgium, April 2014, 2016. Springer, 423–436.