Path Space Filtering
1 Summary
本文提出一种在path space对着色点平滑邻近区域的光线路径的算法,提高光线传播的蒙特卡洛追踪过程的效率。提出的平滑算法基于光子映射框架,采样着色点附近的光线路径,并基于几何、材质、可见性等方面的相似性设计平滑权重。
2 Background
2.1 Particle Tracing
particle tracing算法从光源出发,进行追踪,与表面相交时在交点放置能量,然后再进行反射。与之相对的是path tracing,从相机出发,为每个像素采样光线样本。particle tracing算法生成一批样本,表示一点 $p_j$ 收到来自方向 $\omega_j$ 的throughput weight $\beta_j$ 如下所示
$$
(p_j, \omega_j, \beta_j)
$$
其中,$\beta_j$ 为throughput与采样概率密度的比值,这个采样概率密度指的是? :confused: 。
throughput与flux/功率类似,但不是物理量,指的是某一时刻光子携带的能量,例如经过一次反射后会乘上BSDF系数,相当于scaled radiance。那么 $\beta_j$ 也就是 $f\cdot radiance / pdf=f\cdot L_i / p$ 正好是蒙特卡洛积分的重要性采样形式。
基于tracing阶段得到的particle,我们可以计算任意测量的估计。测量量使用重要性函数 $W_e(p,\omega)$ 来描述,$W_e$应该满足测量量的定义与估计量之间的无偏,
$$
E\left[\frac{1}{N}\sum_{j=1}^N\beta_jW_e(p_k,\omega_j)\right]=\int_A\int_{S^2}W_e(p,\omega)L_i(p,\omega)|\cos\theta|\space \mathrm{d}\omega \mathrm{d}A \label{importance-func} \tag{1}
$$
其实就是将半球面上的积分再嵌套一层表面上点的积分,最外层嵌套 ($\mathrm{d}A$) 就是为了对所有粒子上的测量,而内层 ($\mathrm{d}\omega$) 是在着色点半球面内的测量,可以理解为粒子框架下的渲染方程。
2.1.1 例子:测量墙的入射通量
以测量一面墙入射的通量为例,该通量定义如下
$$
\Phi = \int_{A_{wall}}\int_{H^2(\mathbf{n})}L_i(p,\omega)|\cos\theta|\space \mathrm{d}A\mathrm{d}\omega
$$
对于该测量可以定义如下重要性函数,用来选取位于墙上并且来自normal方向定义的半球区域的入射部分:
$$
W_e(p,\omega)=\begin{cases}\begin{align}
& 1 \quad \quad \text{p is on wall and } (\omega\cdot \mathbf{n}) > 0\
& 0 \quad \quad otherwise
\end{align}\end{cases}
$$
如果 $\eqref{importance-func}$ 式满足,那么上述测量量就可以使用粒子加权和形式来估计。如果想要测量另一面墙 (或者墙的一部分) 的通量,我们可以重新定义 $W_e$,只需要重新计算粒子的加权和即可,粒子可以重复利用。
2.2 Photon Mapping
为了计算 $p$ 点在 $\omega_o$ 方向上反射的radiance,可以等价地表示为对场景表面的所有点的测量,其中Dirac delta分布仅选择精确在 $p$ 点处的粒子,如下式
$$
\int_{S^2}L_i(p,\omega_i)f(p,\omega_o,\omega_i)|\cos\theta_i|\space\mathrm{d}\omega_i = \int_A\int_{S^2}\delta(p-p’)L_i(p’,\omega_i)f(p’,\omega_o,\omega_i)|\cos\theta_i|\space\mathrm{d}\omega_i\mathrm{d}A(p’) \label{exit-radiance} \tag{2}
$$
左边是 $p$ 点处的渲染方程,右边是一种转为对表面点积分的等价表示。按照 $\eqref{importance-func}$ 式,可以得到描述测量量的重要性函数
$$
W_e(p’,\omega)=\delta(p’-p)f(p,\omega_o,\omega_i) \label{pm-importance-func} \tag{3}
$$
光子映射引入的有偏近似:基于附近点的光照信息可以看作着色点的照明的合理近似的假设,提出在着色点周围的光子中进行插值来提供着色点接收的光照信息。因此,$\eqref{pm-importance-func}$ 式的delta分布可以替换为一种filter函数。
2.2.1 光子映射算法
光子映射是一种particle tracing算法,其过程是2-pass算法:
- light pass:光源发出光子,光子与表面相交的信息存储在kd-tree结构上(光子贴图)。存储的信息用于后面的着色,包括光子位置、方向以及throughput。
- camera pass:由相机出发的光路,光路顶点即为着色点。每个光路顶点在光子贴图中查找其周围的光子信息,进行加权着色。
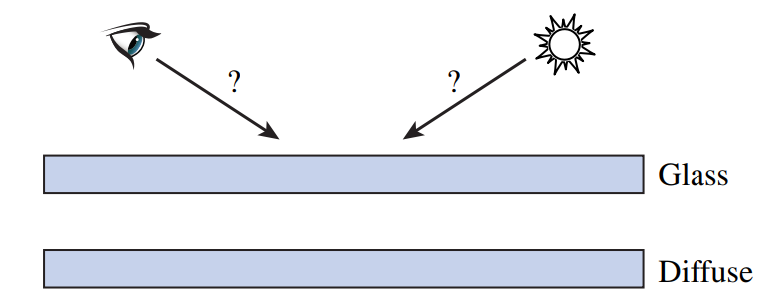
光子映射的优点:光子可以被重用以及开销容易被分摊;着色点使用附近的光子提供光照,更容易解决无偏算法 (例如path tracing、BDPT等) 中无法基于增量路径构建的路径采样问题。例如如下场景,针孔相机与场景之间有一块能折射光线的玻璃板,以及场景中的点光源。没有能够采样到一个能够到达点光源的入射方向的采样策略。但光子映射可以通过追踪由光源出发后在diffuse表面沉淀的光子,着色点附近的光子可以用来很好地估算照明。
传统的path tracing选择与点光源直接相连,但中间光路会由于折射被改变,会导致这样采样得到的方向并不能到达光源。还要在求交后再进行调整,调整后再求交。
2.2.2 Density Estimation
使用着色点附近的光子进行照明的一个统计方法density estimation:即先假设这些样本来自同一个总体分布,构造该组样本点的概率密度函数(PDF)。比如直方图这一简单例子,1D情况下可以划分等宽区间,然后计算每个区间的样本数量,最后进行归一化得到概率密度。
kernel method
kernel method可以得到更加平滑的PDF,给定核函数(kernel function) $k(x)$,有 $\int_{-\infin}^{+\infin} k(x)\mathrm{d}x = 1$。对于 $N$ 个样本,在$x_i$ 处的的核估计量(kernel estimator)为
$$
\hat{p}(x)=\frac{1}{Nh}\sum_{i=1}^N k\left(\frac{x-x_i}{h}\right) \label{kernel-estimator} \tag{4}
$$
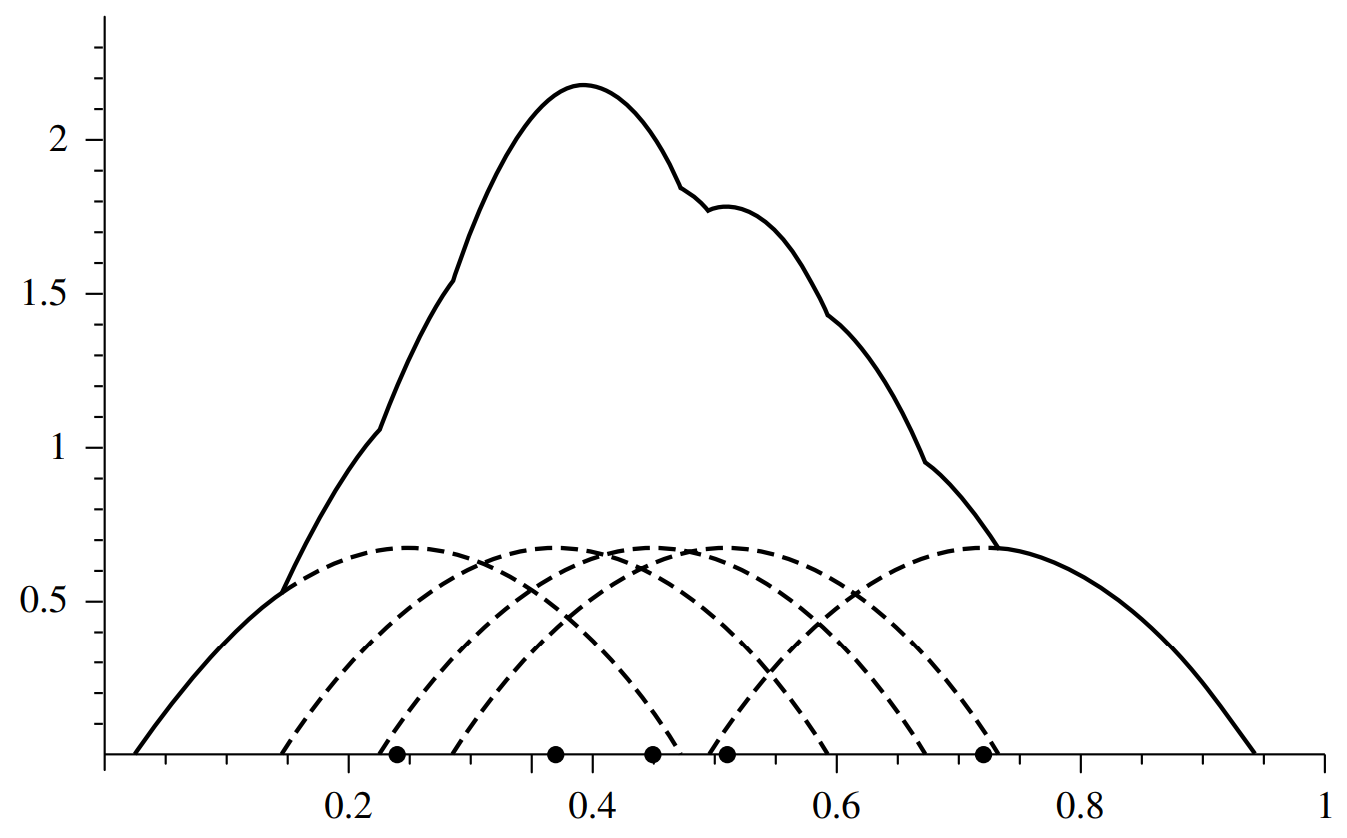
其中,$h$ 是窗口大小(window width)(或者平滑参数、kernel bandwidth)。给定 $N$ 个样本,核估计就是在每个样本上应用核估计函数,然后将这些核函数值加起来形成整体的密度估计。下图就是1D下应用 Epanechnikov kernel 的示例,核函数为
$$
k(t) =
\begin{cases}
0.75(1-2t^2)/\sqrt{5}, \quad t < \sqrt{5} \
0,\quad otherwise
\end{cases}
$$
图中每条圆弧形虚曲线都对应在某一点处的核估计,所有核估计形成实线形状的整体密度估计
2.2.3 nth nearest neighbor estimate
kernel method的关键问题是 $h$ 的选取,太宽会模糊具有许多样本的区域的相关细节;太窄会导致PDF在尾部的分布由于样本不够而凹凸不平。Nearest-neighbor 基于局部样本密度来自适应选择窗口大小,附近样本越多,窗口越小;反之,窗口越大。
nth nearest neighbor estimate 选择 $Nth$ nearest 样本到估计点 $x$ 的距离 $d_N(x)$ 作为窗口大小,代入到 $\eqref{kernel-estimator}$ 有
$$
\hat{p}(x)=\frac{1}{Nd_N(x)}\sum_{i=1}^Nk\left(\frac{x-x_i}{d_N(x)}\right)
$$
扩展到 $d$ 维,有
$$
\hat{p}(x)=\frac{1}{N(d_N(x))^d}\sum_{i=1}^Nk\left(\frac{x-x_i}{d_N(x)}\right) \label{density-estimate} \tag{5}
$$
将密度估计代入到 $p$ 点在出射方向 $\omega_o$ 上的出射radiance测量 $\eqref{exit-radiance}$ ,能够得到以下估计量
$$
L_o(p, \omega_o) \approx \frac{1}{N_p(d_N(p))^2}\sum_{j=1}^{N_p}k\left(\frac{p-p_j}{d_N(p)}\right)\beta_jf(p,\omega_o,\omega_j) \label{exit-radiance-pm} \tag{6}
$$
其中 $N_p$ 表示光子数量,重要性函数使用密度估计方程代替,同时对于超出 N nearest距离的采样点,核函数为0。这个估计过程是先在 $p$ 点的 tangent plane 上采样一点 $p_j$ (即内层积分的 $p’$),因此这里的密度估计是2维。如前所述,$\beta_j$ 是 $p$ 在入射方向 $\omega_j$ 收到的 throughput与采样概率密度(渲染方程积分的采样)的比值。注意观察与标准渲染方程积分估计的区别:
- 渲染方程积分采样点永远是着色点,而这里近似为了着色点附近区域以某一密度估计下的采样点。这是一种着色点邻近区域的插值过程。
- 如果将着色点附近区域内的采样改为(着色点处为1,其余为0)的分布,上式恰好可以退化为渲染方程
$\eqref{exit-radiance-pm}$ 在光子上的测量是一种插值过程,该过程引入的偏差难以估计,但通过提高光子密度往往可以得到更好的结果。如果直接光照使用传统方式,而对于更加低频的间接光通常问题不大。
$\eqref{exit-radiance-pm}$ 式过程的理解,$\eqref{exit-radiance-pm}$ 是对以下积分的近似:
$$
\int_{S^2}L_i(p,\omega_i)f(p,\omega_o,\omega_i)|\cos\theta_i|\space\mathrm{d}\omega_i = \int_A\int_{S^2}\hat{p}(p’)L_i(p’,\omega_i)f(p’,\omega_o,\omega_i)|\cos\theta_i|\space\mathrm{d}\omega_i\mathrm{d}A(p’)
$$
particle tracing与path tracing的不同,导致二者在求渲染方程积分上不同
- path tracing:从着色点出发,采样不同的光线,对光线交点着色得到光线方向上的入射radiance。光线相交于表面后,再采样下一级反射方向,递归执行。
- particle tracing:从光源出发,
每个光子携带了其从光源传播到当前位置整条光路累积后的 $f \cdot radiance / pdf$。光子映射本质上是采样着色点周围的光子,作为着色点的近似,是一种filter过程。因此渲染方程则近似为了对光子的加权平均,权重与光子的分布有关
从上式积分形式看,外层是对表面上(着色点附近)光子的积分,而内层积分则是对于光子 $p’$ 的 $\beta$ 积分。
[2.2.1 光子映射算法](#2.2.1 光子映射算法) 小节描述的最初形式的光子映射算法先进行光子生成,存放到光子贴图上;再进行测量过程。这会导致光子数量受存储空间限制,当存储耗尽时,质量就无法再进一步提高,限制了算法上限。
2.3 Progressive Photon Mapping (PPM)
PPM算法重构了最初形式的光子映射,避免光子存储带来的限制,同样也是2-pass算法:
- camera pass:追踪从相机出发的光路,直至第一个diffuse表面,记录下来交点(visible point)几何信息以及漫反射,同时累积光路经过的specular表面的BSDF。
- light pass:从光源发出光子光路(多级),每一级光子与表面的相交时,都会向其周围的visible points贡献radiance估计
这种方法不需要存储光子,只需要存储camera pass得到的visible point,这部分要远小于记录场景的光子贴图。但对于高分辨率以及需要高SPP的情况下,存储开销依然较高。
2.4 Stochastic Progressive Photon Mapping (SPPM)
SPPM对PPM进一步改进,做到不受内存限制的影响。SSPM依然是从camera pass出发,但其限制了每像素的采样数(可以低至1SPP),即visible points的存储固定;之后light pass同样是从光源出发,使用光子对周围visible points贡献radiance。不同的是,SPPM将这个过程迭代执行,使用同样的visible points存储达到高SPP的结果。
SPPM 同样基于 $\eqref{exit-radiance-pm}$ 光子估计方程出发,但存在两个调整。首先它使用常数核函数,估计过程发生在visible point的tangent平面,$p$ 点在 $\omega_o$ 方向的出射radiance估计量如下,
$$
L_o(p,\omega_o)\approx \frac{1}{N_p\pi r^2}\sum_j^{N_p}\beta_jf(p,\omega_o,\omega_j) \label{constant-estimate} \tag{6}
$$
其中,$N_p$ 是光源发出的光子数量;$\pi r^2$ 是盘形 (disk-shaped) 核函数的表面积。
第二个调整是每次迭代逐步减小光子的搜索半径。这种做法的总体想法是,随着搜索半径内发现的光子数量增多,会有更多证据表明足够的光子密度可以很好估计入射分布;通过减小半径,可以更偏向于细节保留。而当减小半径时,意味着累积的光子来自不同的半径范围,那么同样需要对此进行调整。下面的更新规则描述了如何更新半径以及依赖的变量:
$$
\begin{align}
N_{i+1} &= N_i + \gamma M_i \
r_{i+1} &= r_i\sqrt{\frac{N_{i+1}}{N_i+M_i}} \
\tau_{i+1} &= (\tau_i + \Theta_i)\frac{r^2_{i+1}}{r^2_i}
\end{align}
$$
其中,$N_i$ 是 i-th 迭代之前的贡献给着色点的光子总数;$M_i$ 是当前迭代贡献的光子数量;$r_i$ 是i-th迭代的搜索半径;$\gamma$ 是用于调整收缩速度的超参,通常选择 2/3;$\tau$ 是BSDF的累积;$\Theta_i$ 在i-th迭代的计算如下,即当前迭代光子的throughput之和。
$$
\Theta_i = \sum_j^{M_i}\beta_jf(p,\omega_o,\omega_j)
$$
3 Approach
本文提出的path space filter算法过程如下图所示:绿色部分展示了通过filter顶点 $x_i$ 的球邻域 $\mathcal{B}(n)$ 中顶点收到的光路贡献 $c_{s_i+j}$ 来近似到 $x_i$ 的光路贡献 $c_i$ ,其中 $\alpha_i$ 为 $x_i$ 到相机方向的衰减系数。
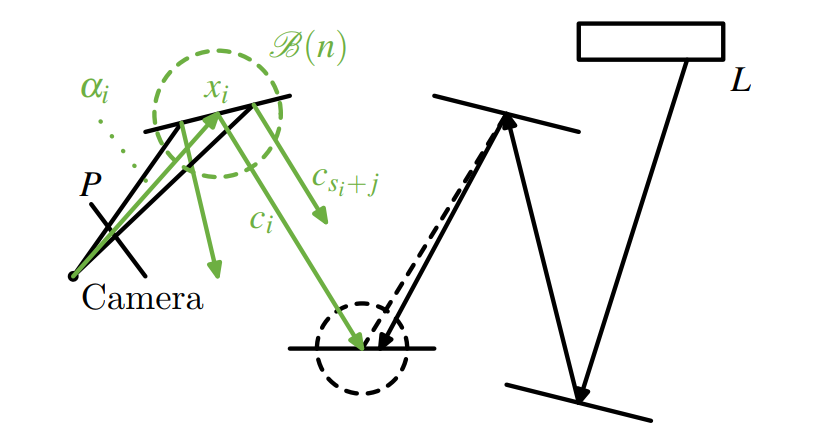
图像上像素计算为累积 $\alpha_i\cdot \bar{c_i}$,即累积每根采样光线
$$
\bar{c_i} = \frac{\sum_{j=0}^{b^m-1} \mathcal{X}{\mathcal{B}(n)}(x{s_i+j} - x_i) \cdot w_{i,j} \cdot c_{s_i+j}}{\sum_{j=0}^{b^m-1} \mathcal{X}{\mathcal{B}(n)}(x{s_i+j} - x_i)\cdot w_{i,j}} \label{path-filter} \tag{7}
$$
其中 $ \mathcal{X}{\mathcal{B}(n)}$ 为特征函数,在数学上也称为指示函数(indicator function),这里意义为:位于球内为1;否则为0。 $\eqref{path-filter}$ 式遍历以 $x_i$ 为中心、半径为 $r(n)$ 的领域 $\mathcal{B}(n)$ 内的所有顶点 $x{s_i+j}$,对每个顶点的光路贡献 $c_{s_i+j}$ 进行加权平均,得到 $\bar{c_i}$ 。其中 $n$ 为每个像素的光线总数,在每次迭代 1spp 的情况下(每次filter都会为像素采样一根光线),也可视为filter迭代次数。$\eqref{path-filter}$ 式的filter过程可以迭代执行,例如再由 $\bar{c_i}$ 计算 $\bar{\bar{c_i}}$,虽然高效,但光照细节被一定模糊,如下图

在迭代filter过程中,随着迭代次数,filter半径逐渐降低,初始半径为 $r_0$,以及参数 $\alpha \in (0, 1)$
$$
r(n) = \frac{r_0}{n^{\alpha}}
$$
因此,随着迭代次数的增加,filter半径逐渐减少,filter区域逐渐消失,有 $\lim_{n\rightarrow \infty}\bar{c_i}=c_i$ 。
3.1 Weighting by Similarity
一些降噪处理中,当光线于物体相交时,通常会根据交点材质来选择是否增加更多光线降低噪声,这被称为 trajectory splitting。$\eqref{path-filter}$ 式中的权重 $w_{i,j}$ 需要评估光路贡献 $c_{s_i+j}$ 通过轨迹分割在 $x_i$ 上被创建的可能性。下图是 path tracer结果、path filter后的结果,以及不同权重选择的效果对比。

3.1.1 Blur across geometry
使用点 $x_i$ 与 $x_{s_i+j}$ 的法线相似度 $(n_i \cdot n_{s_i+j})$,实现中,只会选择 $(n_i \cdot n_{s_i+j}) \geq 0.95$ 的采样点。
3.1.2 Blur across textures
表面材质属性。比较 $x_i$ 与 $x_{s_i+j}$ 的材质属性差异,例如 BSDF。进选择低于阈值的采样点。
3.1.3 Blurred shadows
光源可见性的处理。
对于点光源而言,点光源的阴影边缘是锐利,因此为了不模糊阴影边缘,选择仅会选择可见性一致的采样点。
对于ao或者环境光,可以通过比较进入 $x_i$ 与 $x_{s_i+j}$ 的半球面的光线长度差异,仅选择差异在阈值内的采样点。
3.2 Range Search
$\eqref{path-filter}$ 式中的特征函数 $\mathcal{X}{\mathcal{B}(n)}(x{s_i+j} - x_i)$ 用于在 $x_i$ 的邻域 $\mathcal{B}(n)$ 中选择 $x_{s_i+j}$ 。该过程涉及到的range search可以使用 hash grid、bvh或者kd-tree结构来实现高效查询。
Reference
[1] Alexander Keller, Ken Dahm, and Nikolaus Binder. 2016. Path space filtering. In Monte Carlo and Quasi-Monte Carlo Methods: MCQMC, Leuven, Belgium, April 2014, 2016. Springer, 423–436.
[2] Pharr, M., Jakob, W., Humphreys, G., 2017. Physically based rendering: from theory to implementation. EBSCO eBooks. 963~972.