Projection Transformations
1 Summary
本文介绍投影变换的计算，包括正交投影、透视投影。最后介绍一些实际应用中的技巧、以及如何运用到 Vulkan 坐标系。
Settings：本文的向量采用列向量，与 glm 库的默认为列主序一致，只需将本文描述的公式整体转置即可转为行向量形式；clip 空间的深度值范围采用与 OpenGL 的 $[-1,1]$ ；相机 forward 方向为 $-z$，up 方向为 $+y$ 。相机坐标系与正交投影的长方体视锥体 如下图所示：
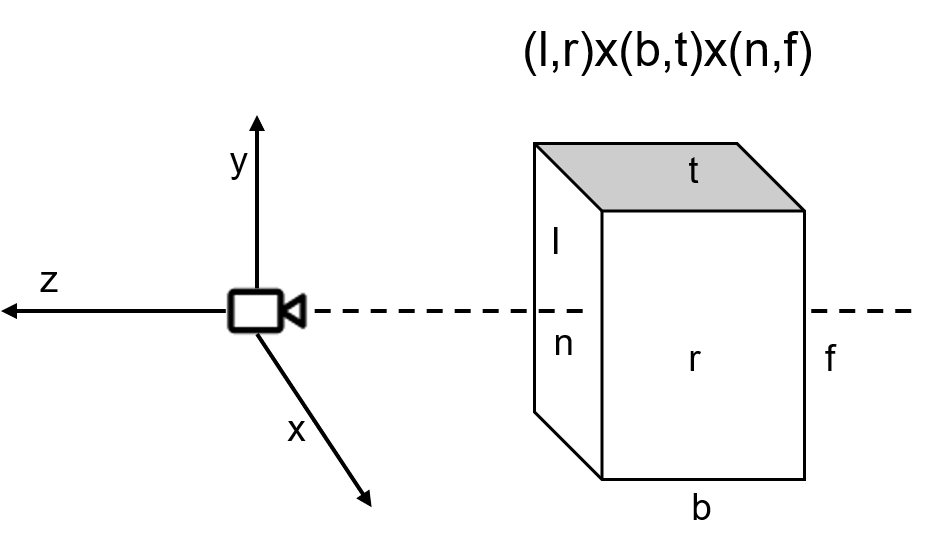
其中 $l,r$ 为 $x$ 轴方向的左右表面到视锥体中心的距离，$b,t$ 为 $y$ 轴方向的上下表面到视锥体中心的距离，$n,f$ 为 $z$ 轴方向的前后表面到原点的距离(即近平面与远平面)。相机坐标系采用 Vulkan 的右手坐标系。注意：近平面 $n$ 并不是成像屏幕，只是裁剪平面，这个裁剪平面的大小由fov与近平面z值决定。
2 Orthographic Projection
正交投影将 $(-l,r)\times(-b,t)\times(-n,-f)$ 的视锥体变换为 $(-1,1)\times(-1,1)\times(-1,1)$。注意：通常情况下正交投影的视锥体定义为关于 $z$ 轴对称，即 $l=r,b=t$，在本文最后结果对应替换即可。正交投影的过程可分为两步：先将视锥体近平面的中心平移至相机坐标系的原点；再将大小进行缩放。
2.1 视锥体的中心平移至原点
视锥体中心坐标为 $\large \left(\frac{r-l}{2},\frac{t-b}{2},-\frac{n+f}{2}\right)$，因此构建平移矩阵
$$
M_{orthoT}=
\begin{pmatrix}
1 & 0 & 0 & \frac{l-r}{2} \
0 & 1 & 0 & \frac{b-t}{2} \
0 & 0 & 1 & \frac{n+f}{2} \
0 & 0 & 0 & 1
\end{pmatrix}
$$
验证一下：对于左右表面的 $x$ 坐标，左表面 $x$ 坐标变换前 $-l$，有 $-l+\frac{l-r}{2}=\frac{-l-r}{2}$ ；右表面 $x$ 坐标变换前 $r$，有 $r+\frac{l-r}{2}=\frac{l+r}{2}$ 。变换后的 $x$ 坐标对称。
对于近平面，变换前 $-n$，有 $-n+\frac{n+f}{2}=\frac{f-n}{2}$；对于远平面，变换前 $-f$，有 $-f+\frac{n+f}{2}=\frac{n-f}{2}$
2.2 frustum 进行缩放
经过平移后的视锥体为 $(\frac{-l-r}{2},\frac{l+r}{2})\times(\frac{-b-t}{2},\frac{b+t}{2})\times(\frac{n-f}{2},\frac{f-n}{2})$，将平移后的视锥体缩放为
$(-1,1)\times(-1,1)\times(-1,1)$，构建缩放矩阵
$$
M_{orthoS}=
\begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & 0 \
0 & \frac{2}{b+t} & 0 & 0 \
0 & 0 & \frac{2}{f-n} & 0 \
0 & 0 & 0 & 1
\end{pmatrix}
$$
至此就完成了构建正交投影矩阵
$$
M_{ortho} = M_{orthoS} \cdot M_{orthoT}
$$
3 Perspective Projection
透视投影为了模拟现实中近大远小，采用截去头部的金字塔形状的 frustum，如下图所示
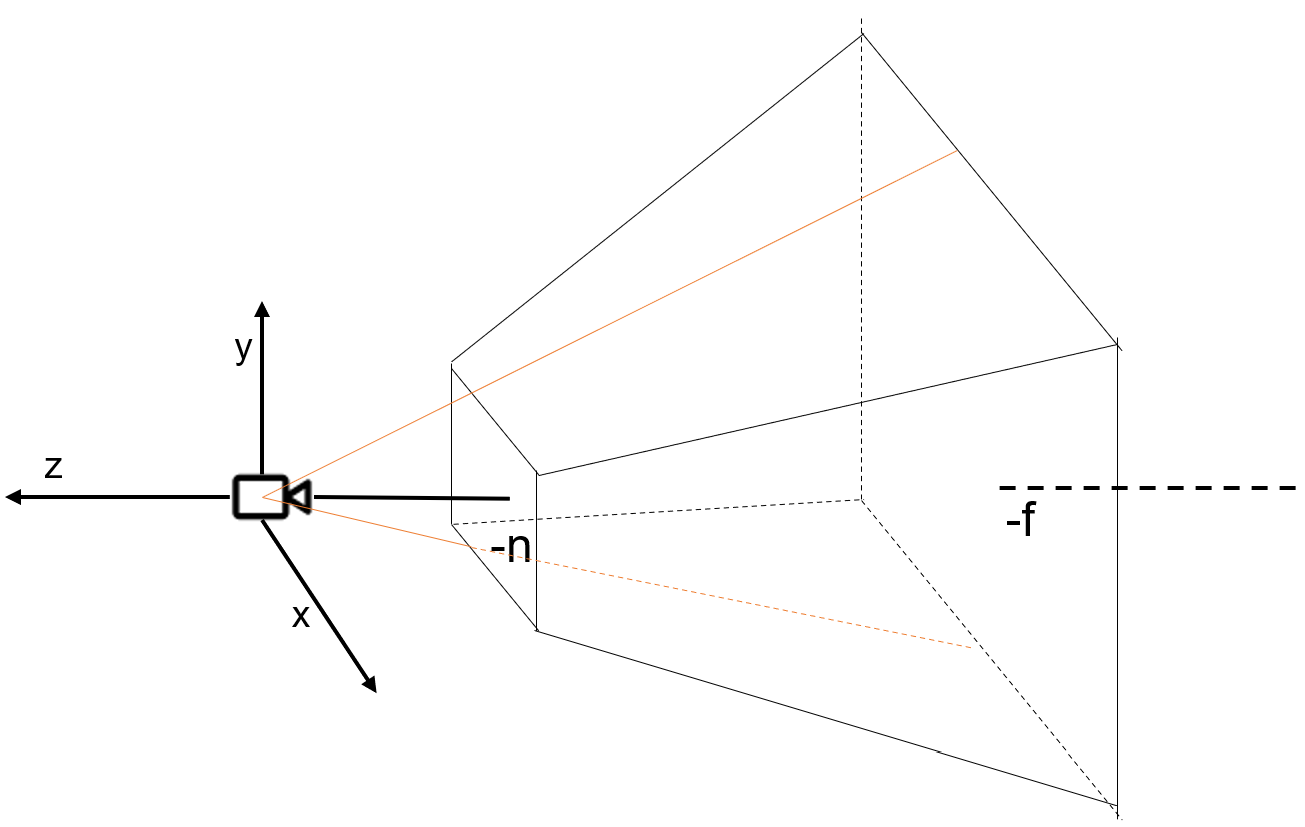
右图为左图的二维投影，透视投影的 frustum 是通过 fov 参数定义，所以是右图中过原点的情况，其中 $n,f$ 分别是近平面和远平面。
求解透视投影的投影矩阵可以分为两步：将透视投影的视锥体变形为正交投影的视锥体；再进行正交投影变换。
3.1 frustum 视锥体挤压为长方体视锥体
3.1.1 一般情况推导出变换矩阵的部分元素
将 frustum 远平面四个角进行挤压，将远平面变形为与近平面一样大小。假设变形前 frustum 内任一点为 $(x,y,z)$，变形为 $(x’,y’,z’)$ 。变换前后的点有如下关系:
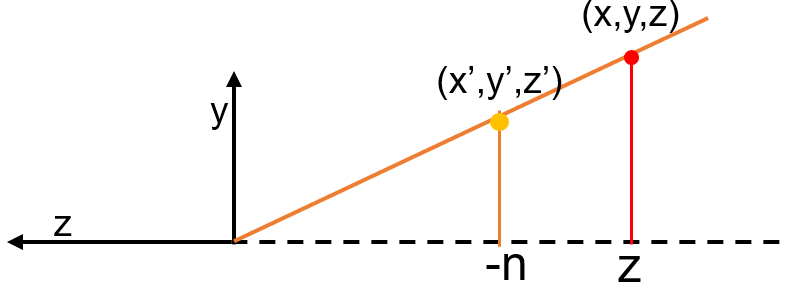
朝 $-x$ 方向看去的平面图，可以根据相似三角形有(注意使用边长)：
$$
\frac{y’}{y}=\frac{-z’}{-z}=\frac{n}{-z}
\
y’=\frac{n}{-z}\cdot y
$$
同理，从 $-y$ 方向看去的平面图，可得到：
$$
\frac{x’}{x}=\frac{n}{-z} \
x’=\frac{n}{-z}\cdot x
$$
注意：对于 $z$ 变换前后是没有直观关系的，经过挤压变形 $z$ 坐标可能前移后移。
此时变换后的坐标为 $(\large \frac{n}{-z}\cdot x,\frac{n}{-z}\cdot y,z’,1)$ ，对于齐次坐标，同时乘上一个坐标，不改变其表示的点，同时乘 $-z$ 有：
$$
(nx,ny,-zz’,-z)
$$
假设 frustum 到长方体的变换矩阵为 $M_{persp->ortho}$，目前已知以下变换成立：
$$
M_{persp->ortho}\cdot (x,y,z,1)^T =(nx,ny,-zz’,-z)^T
$$
有变换前后对应关系可知 $M_{persp->ortho}$ 的第一行可以确定为 $(n,0,0,0)$，第二行可以确定为 $(0,n,0,0)$，第三行未知，第四行可以确定为 $(0,0,-1,0)$。因此，此时
$$
M_{persp->ortho}=
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
? & ? & ? & ? \
0 & 0 & -1 & 0
\end{pmatrix}
$$
3.1.2 代入特殊点得到未知的 $z$ 坐标变换
虽然任意点的 $z$ 坐标变换前后的对应关系不能直观看出，但是对于在近平面和远平面上的点，其 $z$ 坐标变换前后不改变，因此有 $z’=z=-n$。代入近平面，将 $z’=z=-n$ 代入得到变换前的点有 $(x,y,-n,1)$，变换后的点有 $(nx,ny,-n^2,n)$。因此有
$$
M_{persp->ortho}\cdot (x,y,-n,1)^T=(nx,ny,-n^2,n)^T
$$
由变换前后的 $z$ 坐标对应关系，有 $M_{persp->ortho}$ 的第三行前两个元素为 $0$，假设后两个元素为 $C,D$，可以列
$$
-Cn+D=-n^2
$$
代入远平面，将 $z’=z=-f$ 代入得到变换前的点有 $(x,y,-f,1)$ ，变换后的点有 $(nx,ny,-f^2,f)$。因此有
$$
M_{persp->ortho}\cdot (x,y,-f,1)^T=(nx,ny,-f^2,f)^T
$$
可以列
$$
-Cf+D=-f^2
$$
于是有 $C=n+f,D=nf$，于是 frustum 变形为长方体的变换矩阵为：
$$
M_{persp->ortho}=
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
0 & 0 & n+f & nf \
0 & 0 & -1 & 0
\end{pmatrix}
$$
3.2 完整的投影变换矩阵
$$
\begin{align} M_{persp} &= M_{ortho}\cdot M_{persp->ortho}=M_{orthoS} \cdot M_{orthoT}\cdot M_{persp->ortho} \
&=\begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & 0 \
0 & \frac{2}{b+t} & 0 & 0 \
0 & 0 & \frac{2}{f-n} & 0 \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
1 & 0 & 0 & \frac{l-r}{2} \
0 & 1 & 0 & \frac{b-t}{2} \
0 & 0 & 1 & \frac{n+f}{2} \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
0 & 0 & n+f & nf \
0 & 0 & -1 & 0
\end{pmatrix} \
&= \begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & \frac{l-r}{l+r} \
0 & \frac{2}{b+t} & 0 & \frac{b-t}{b+t} \
0 & 0 & \frac{2}{f-n} & \frac{n+f}{f-n} \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
0 & 0 & n+f & nf \
0 & 0 & -1 & 0
\end{pmatrix} \
&= \begin{pmatrix}
\frac{2n}{l+r} & 0 & -\frac{l-r}{l+r} & 0 \
0 & \frac{2n}{b+t} & -\frac{b-t}{b+t} & 0 \
0 & 0 & \frac{n+f}{f-n} & \frac{2nf}{f-n} \
0 & 0 & -1 & 0
\end{pmatrix}
\end{align}
$$
3.2.1 使用 Fov 和 Aspect 简化投影矩阵
fov 为相机在 $y$ 轴方向的视锥范围的角度，由于视锥通常取关于 $z$ 轴对称，$+y$ 轴部分视锥范围为 fov 的一半，如下图所示
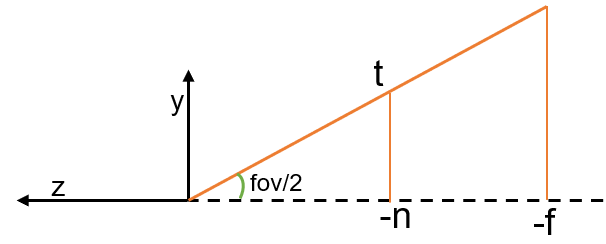
有
$$
\tan \frac{fov}{2}=\frac{t}{n}, \quad t=n\cdot \tan\frac{fov}{2}
$$
由于视锥关于 $z$ 轴对称有 $l=r,t=b$，aspect 为宽高比，即 $aspect = \frac{r}{t}$，因此有
$$
\begin{cases}
\begin{align}
t&=b=n\cdot \tan\frac{fov}{2} \
l&=r=aspect\cdot n \cdot tan\frac{fov}{2}
\end{align}
\end{cases}
$$
代入矩阵 $M_{persp}$ 中有
$$
M_{persp}=\begin{pmatrix}
\frac{1}{aspect\cdot \tan\frac{fov}{2}} & 0 & 0 & 0 \
0 & \frac{1}{\tan\frac{fov}{2}} & 0 & 0 \
0 & 0 & \frac{n+f}{f-n} & \frac{2nf}{f-n} \
0 & 0 & -1 & 0
\end{pmatrix}
$$
3.3 对于深度范围为 [0,1] 的投影变换
Direct3D 与 Vulkan 的深度范围为 $[0,1]$，因此对应 clip space 的 view volume 为 $(-1,1)\times(-1,1)\times(0,1)$。因此需要修改正交投影变换：
首先将视锥体的近平面中心点平移至原点，近平面中心点坐标为 $\large \left(\frac{r-l}{2},\frac{t-b}{2},-n\right)$
$$
M_{orthoT}=
\begin{pmatrix}
1 & 0 & 0 & \frac{l-r}{2} \
0 & 1 & 0 & \frac{b-t}{2} \
0 & 0 & 1 & n \
0 & 0 & 0 & 1
\end{pmatrix}
$$然后缩放平移后的视锥体 $(\frac{-l-r}{2},\frac{l+r}{2})\times(\frac{-b-t}{2},\frac{b+t}{2})\times(0,-(f-n))$ 为 $(-1,1)\times(-1,1)\times(0,1)$
$$
M_{orthoS}=
\begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & 0 \
0 & \frac{2}{b+t} & 0 & 0 \
0 & 0 & -\frac{1}{f-n} & 0 \
0 & 0 & 0 & 1
\end{pmatrix}
$$最后的投影变换为
$$
\begin{align} M_{persp} &= M_{ortho}\cdot M_{persp->ortho}=M_{orthoS} \cdot M_{orthoT}\cdot M_{persp->ortho} \
&=\begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & 0 \
0 & \frac{2}{b+t} & 0 & 0 \
0 & 0 & -\frac{1}{f-n} & 0 \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
1 & 0 & 0 & \frac{l-r}{2} \
0 & 1 & 0 & \frac{b-t}{2} \
0 & 0 & 1 & n \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
0 & 0 & n+f & nf \
0 & 0 & -1 & 0
\end{pmatrix} \
&= \begin{pmatrix}
\frac{2}{l+r} & 0 & 0 & \frac{l-r}{l+r} \
0 & \frac{2}{b+t} & 0 & \frac{b-t}{b+t} \
0 & 0 & -\frac{1}{f-n} & -\frac{n}{f-n} \
0 & 0 & 0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
n & 0 & 0 & 0 \
0 & n & 0 & 0 \
0 & 0 & n+f & nf \
0 & 0 & -1 & 0
\end{pmatrix} \
&= \begin{pmatrix}
\frac{2n}{l+r} & 0 & -\frac{l-r}{l+r} & 0 \
0 & \frac{2n}{b+t} & -\frac{b-t}{b+t} & 0 \
0 & 0 & \frac{f}{n-f} & \frac{nf}{n-f} \
0 & 0 & -1 & 0
\end{pmatrix}
\end{align}
$$代入 fov 与 aspect 简化有
$$
M_{persp}=\begin{pmatrix}
\frac{1}{aspect\cdot \tan\frac{fov}{2}} & 0 & 0 & 0 \
0 & \frac{1}{\tan\frac{fov}{2}} & 0 & 0 \
0 & 0 & \frac{f}{n-f} & \frac{nf}{n-f} \
0 & 0 & -1 & 0
\end{pmatrix}
$$
3.4 透视投影非线性
透视投影具有非线性的性质，其非线性是由于最后的齐次坐标除以 $w$ 分量 (divide z) 引入的。这里我们只需关注 $w$ 分量的变换操作，因此只需关注透视投影矩阵变换的第四行。对于原坐标 $(x,y,z,1)$，经过透视变换后的 $w$ 分离由 $1$ 变为 $z$，即变换后的点为 $(x’,y’,z’,z)$。
非线性带来的问题
顶点面片光栅化为像素的插值操作，是以三角面片在像素点的重心坐标为参数进行插值的，这个过程是线性过程。但由于投影变换引入了非线性，在三维空间线性变化的顶点属性，经过投影变换，在屏幕空间并不是线性变化，因此不能直接使用重心坐标进行顶点属性的插值。如下图所示：
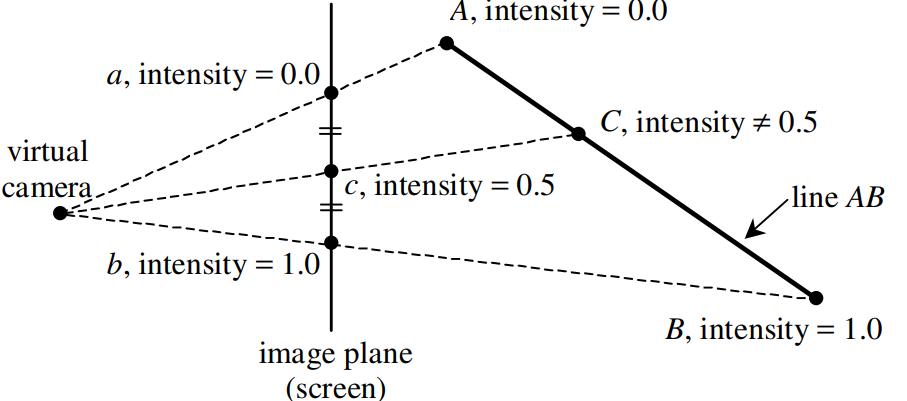
三维空间的线 $AB$，投影到屏幕空间 $ab$。$ab$ 的中点对应的却不是 $AB$ 的中点。
为了解决透视投影带来的非线性问题，插值引入了 perspective-correct interpolation，目前 vertex shader 到 pixel shader 的变量，默认都为 perspective-correct interpolation。
4 Practical Tricks
4.1 $w$ 分量归一化与 divide z
在 shader 中，对坐标进行透视投影后进行齐次坐标 $w$ 分量归一化时，除以 $w$ 和除以 $z$ 分量都一样，因为透视投影得到的 $w$ 分量与 $z$ 恒有 $w=z$ （或 $w=-z$，依赖于推导过程）。
4.2 屏幕空间的像素坐标到相机空间的逆变换
在某些算法中，经常需要从屏幕像素坐标恢复到相机空间的坐标。
在 pixel shader 中进行逆投影变换（低效）
使用透视投影的逆矩阵可以直接做到，如
$$
inverse(M_{persp})\cdot (clip.x,clip.y,clip.z)
$$
vertex shader 中进行 $(x,y)$ 逆变换，pixel shader 中进行 depth 逆变换（高效）
直接在 pixel shader 中进行逆投影变换，较为低效，可以在 vertex shader 中计算。对于具有顶点输入的 pass，vertex shader 中只进行 view transform，不进行透视变换，此时变换后的顶点还处于三维线性空间中，即变换后的 $w$ 分量还是 $1$，因此到 pixel shader 的插值还是线性插值。
多数情况是 postprocess 的算法，vertex shader 只是 quad 绘制，没有顶点信息。可以在 vertex shader 中 quad 绘制得到的 texcoord 坐标进行逆透视投影，转到 view space 中，此时只需要传逆变换后的 $( x,y)$ 坐标到 pixel shader。在 pixel shader 中，只将 depth 信息变换回 view space。只是 depth 的逆变换，不需要对整个透视投影进行求逆。变换前点为 $(x,y,z,1)$，有投影变换（使用深度范围 [0,1] 的投影变换）：
$$
\begin{align}
M_{persp}\cdot (x,y,z,1)^T &=\begin{pmatrix}
\frac{1}{aspect\cdot \tan\frac{fov}{2}} & 0 & 0 & 0 \
0 & \frac{1}{\tan\frac{fov}{2}} & 0 & 0 \
0 & 0 & \frac{f}{n-f} & \frac{nf}{n-f} \
0 & 0 & -1 & 0
\end{pmatrix} \cdot (x,y,z,1)^T \
&=\left(\frac{x}{aspect\cdot \tan\frac{fov}{2}}, \frac{y}{\tan\frac{fov}{2}}, \frac{f\cdot z + nf}{n-f}, -z\right)^T
\end{align}
$$
即变换后的像素深度$0<n<f,-f<z<-n<0,0<clip.z<1$
$$
\begin{align}
clip.z &= \frac{f\cdot z + nf}{n-f}\cdot \frac{1}{-z} = \frac{f\cdot (z+n)}{z\cdot(f-n)} = (1+\frac{n}{z})\cdot \frac{1}{1-\frac{n}{f}} = (1-\frac{n}{-z})\cdot \frac{1}{1-\frac{n}{f}} \
z &=\frac{-nf}{(n-f)clip.z+f}
\end{align}
$$
pixel shader 中只需要进行上式对 $z$ 的逆变换，即 Linearize Depth。
pixel shader中进行逆投影变换
通过矩阵变换可以求都逆投影矩阵 $InvM_{persp}$，逆投影变换有
$$
\begin{align}
& \quad InvM_{persp} \cdot (clip.x, \space clip.y, \space clip.z, \space 1)^T \
&= \begin{pmatrix}
aspect\cdot \tan\frac{fov}{2} & 0 & 0 & 0 \
0 & \tan\frac{f}{2} & 0 & 0 \
0 & 0 & 0 & -1 \
0 & 0 & \frac{n-f}{nf} & \frac{1}{n}
\end{pmatrix} \cdot (clip.x, \space clip.y, \space clip.z, \space 1)^T \
&= (aspect\cdot \tan\frac{fov}{2}\cdot clip.x, \space \tan\frac{fov}{2}\cdot clip.y, \space -1, \space \frac{(n-f)clip.z+f}{nf}) \
&= (aspect\cdot \tan\frac{fov}{2}\cdot clip.x, \space \tan\frac{fov}{2}\cdot clip.y, \space -1, \space -\frac{1}{z}) \
&= (-z\cdot aspect\cdot \tan\frac{fov}{2}\cdot clip.x, \space -z \cdot \tan\frac{fov}{2}\cdot clip.y, \space z, \space 1)
\end{align}
$$
可以看出最后一步除w分量，除得是 $\Large -\frac{1}{z}$。由于是线性变换，因此可以先乘上 $-z$ 避免最后一步除w，即要进行逆变换的坐标为
$$
(-z\cdot clip.x, \space -z\cdot clip.y, \space -z\cdot clip.z, \space -z \cdot 1)
$$注意，如果只取结果xyz分量，最后一个分量乘不乘没有影响，因为 w 分量除了规范化三维坐标没有其他作用，不乘也只是最后得到的 w 分量不是 1 而已
4.3 像素抖动偏移
$$
\begin{align}
M_{persp}\cdot (x,y,z,1)^T &=\begin{pmatrix}
\frac{1}{aspect\cdot \tan\frac{fov}{2}} & 0 & jitter_x & 0 \
0 & \frac{1}{\tan\frac{fov}{2}} & jitter_y & 0 \
0 & 0 & \frac{f}{n-f} & \frac{nf}{n-f} \
0 & 0 & -1 & 0
\end{pmatrix} \cdot (x,y,z,1)^T \
&=\left(\frac{x}{aspect\cdot \tan\frac{fov}{2}} + z\cdot jitter_x, \frac{y}{\tan\frac{fov}{2}}+z\cdot jitter_y, \frac{f\cdot z + nf}{n-f}, -z\right)^T
\end{align}
$$
最后除w得到clip pos，则得到 clip.x 与 clip.y 的偏移量为 $(-jitter_x, -jitter_y)$，因此像素内的抖动值取值范围是 [-1, 1] / resolution
5 任意z处的投影
视锥体每个面的法向量如下图所示，而这些法向量也比较容易得到。首先考虑，投影变换后的 $(-1,1)\times(-1,1)\times(-1,1)$ ，可以得到六个平面方程为
$$
x = \pm1, y = \pm 1,z = \pm 1
$$
将这六个平面法向量代入透视投影逆变换即可。
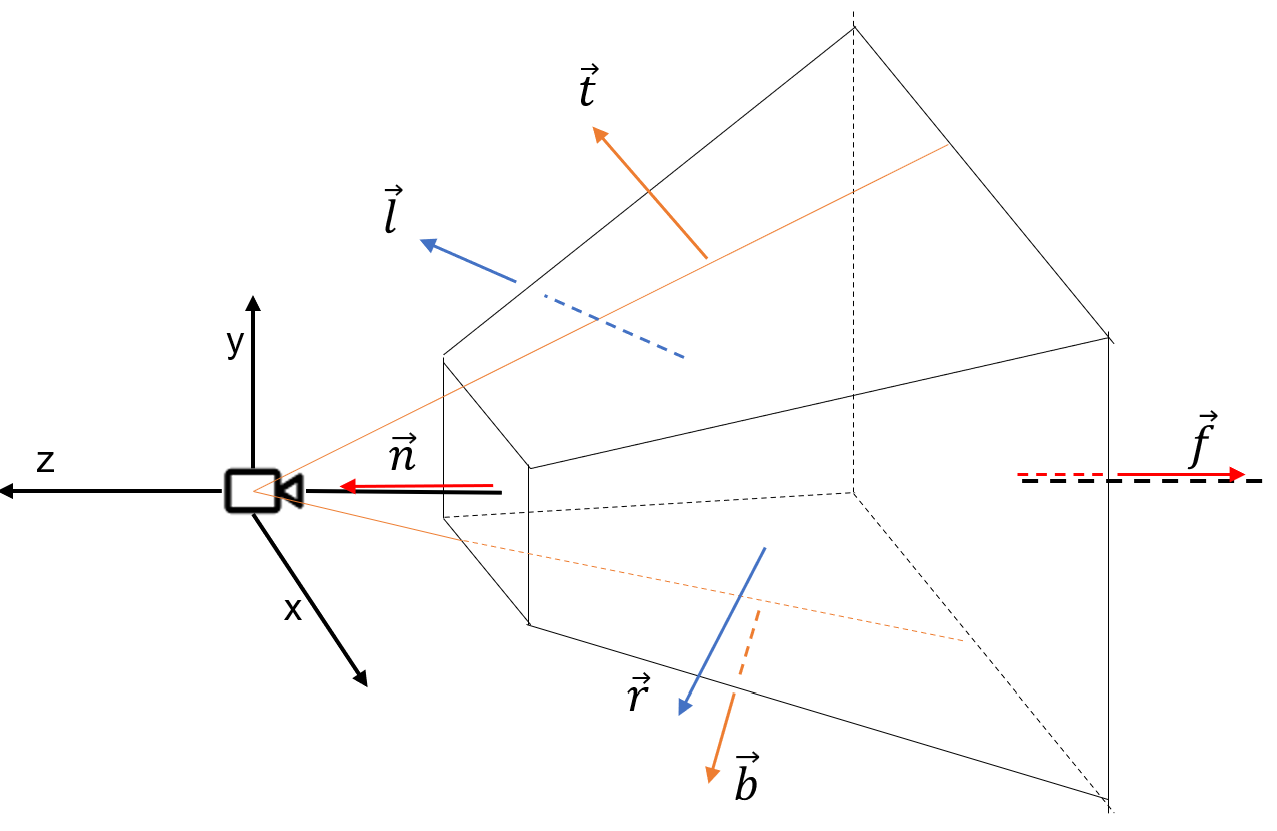
只考虑关于z轴对称的视锥体，因此有 $\vec{l},\vec{r}$ 与 xoz 面平行，$\vec{b},\vec{t}$ 与yoz面平行，$\vec{n}=(0, 0, 1), \vec{f}=(0, 0, -1)$。
只看 xoz 面，如下俯视图
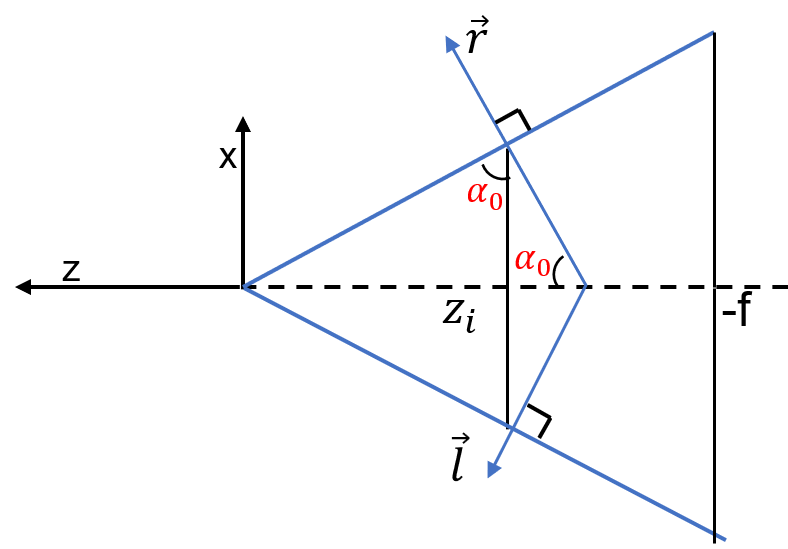
可以得到
$$
\tan\alpha_0=\frac{r.z}{r.x}
$$
对于yoz面，如下侧视图
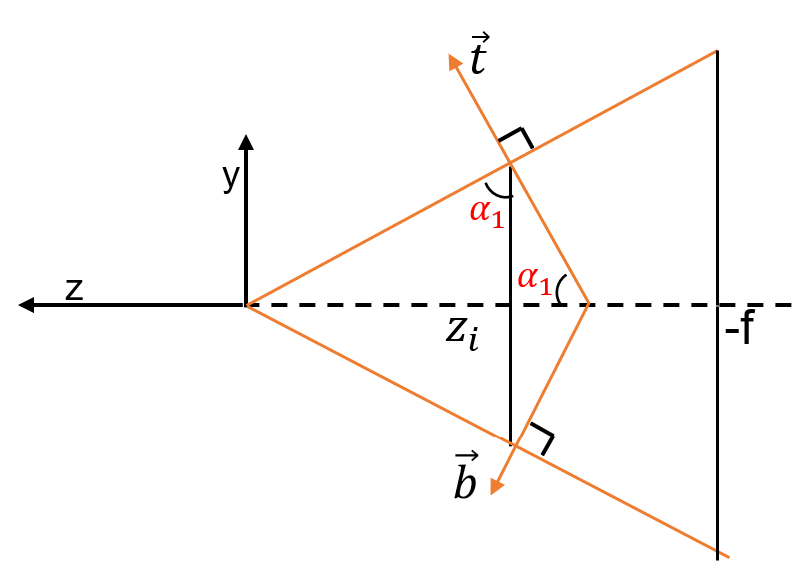$$
\tan\alpha_1=\frac{t.z}{t.y}
$$
那么，在 $z_i$ 处的截面宽、高为
$$
w_i = 2 \cdot z_i \cdot \frac{1}{\tan\alpha_0} \\
h_i = 2 \cdot z_i \cdot \frac{1}{\tan\alpha_1}
$$
至此，我们可以得到视锥体任意截面的大小，这意味着，我们可以将屏幕空间的像素大小逆投影到任意远的截面上。相同的像素大小，在越远的截面上对应区域则越大。
截面位于世界空间，截面的尺度是实际的几何大小，因此假设几何半径 $R_g$，不同尺度间的变换可以通过标准化的中间量 $R_n$，屏幕空间的尺度单位为像素 $R_p$。
因此，投影过程：将 $z_i$ 处的几何半径标准化，再将标准化的半径转为屏幕空间有
$$
\begin{align}
R_{n_x} &= R_g \cdot \frac{1}{w_i} = 0.5 \cdot R_g \cdot \tan\alpha_0 \cdot \frac{1}{z_i} \
R_{n_y} &= R_g \cdot \frac{1}{h_i} = 0.5 \cdot R_g \cdot \tan\alpha_1 \cdot \frac{1}{z_i} \
\
R_{p} &= screenWidth \cdot R_{n_x} \quad or \
R_{p} &= screenHeight \cdot R_{n_y}
\end{align}
$$
逆投影过程：将屏幕空间半径（以像素为单位）先标准化，再转为世界空间的几何半径有
$$
\begin{align}
R_{n_x} &= R_{p} * 1.0 / screenWidth \
R_{n_y} &= R_{p} * 1.0 / screenHeight \
\
R_g &= R_{n_x} * w_i = R_{n_x} * 2.0 * z_i * \frac{1}{\tan\alpha_0} \quad or\
R_g &= R_{n_y} * w_i = R_{n_y} * 2.0 * z_i * \frac{1}{\tan\alpha_1}
\end{align}
$$