Disney BRDF

1 Summary

Disney Principled BRDF 是迪士尼动画工作室在 SIGGRAPH 2012 的 Physically-based shading at Disney [1] 提出。该工作室通过分析 MERL BRDF 材质库，总结出对 microfacet Cook-Torrance BRDF 的各项的观察，如 diffuse、specular D F G等四项。基于观察结论，进一步改进 Cook-Torrance BRDF 模型，并设计出对艺术家友好的参数集。[2] 对这项工作总结得很好，目前不再进行赘述，只追加一些自己新的理解。

2 Cook-Torrance BRDF 的改进

image-20211223113437451 $$ \begin{align} f(\boldsymbol{l},\boldsymbol{v}) = diffuse + \frac{F(\theta_d)\cdot G(\theta_l, \theta_v)\cdot D(\theta_h)}{4\cdot \cos\theta_l\cdot \cos\theta_v} \end{align} \tag{1} \label{Cook-Torrance BRDF} $$

2.1 Diffuse

2.1.1 如何理解漫反射

中学时期漫反射的解释：光照射在非常凹凸不平的物体表面，光线向四面八方反射，可近似看成各个角度均匀反射。但对于微表面模型而言，microfacet BRDF 已经将物体表面看作很多个微表面，对于某一特定方向的入射光，反射到观察方向上的比例，这一反射过程相当于考虑到光在微表面上的 Specular 反射，已经解释了中学时期的所谓的漫反射过程。$\eqref{Cook-Torrance BRDF}$ 中着色模型，分成了 diffuse 项与 微表面模型下的 specular 项，如果采用上述粗浅的漫反射理解，相当于 diffuse 项与 specular 项计算的是相同的东西。

微表面模型下的漫反射的准确理解：光打到物体表面，进入物体表面以下，发生浅层散射，进行多次反射射 (subsurface scattering) ，期间部分光被吸收，剩下的光离开表面。部分光被吸收带来的 diffuse 响应就是表面颜色，被着色的非金属材质的任意出射部分都可以视为 diffuse，可以得知漫反射过程的出射能量比例收到 Fresnel 的影响。

观察结论

  1. grazing retroreflection 情况下，有很明显的着色，即 retroreflective peak。
  2. 出射能量的多少受到 Fresnel 影响，而 roughness 会影响到 Fresnel，因此精准的 diffuse 项需要考虑到 Fresnel 与 roughness。
  3. 粗糙表面的漫反射能量要高于平滑表面的漫反射能量，特别是 grazing retroreflection，粗糙表面出现了一个峰值。

2.1.2 现有 diffuse 模型的不足

  • Lambert Diffuse Model
    Lambert Diffuse Model 假设折射光进行了充足的散射，最终出射的光在所有方向上均匀分布。在距离一定的情况下，漫反射出射的能量由 $(\boldsymbol{n}\cdot\boldsymbol{l})$ 决定，即入射光与红表面法线的夹角越大，出射能量越小。在材质球上的表现为 grazing 角度会较暗，使得材质球边缘有阴影感，视觉上更加立体化。但通过观察，很少有材质与 Lambert Diffuse Model 表现一致。例如，观察 1 中 grazing retroreflection(接近 90° 角) 着色会变强，而不是 Lambert 模型所说，角度越大，出射能量越小。
  • Oren-Nayar Model
    Oren-Nayar Model 有预测到 retroreflective peak，因此 grazing 角度相较于 Lambert 模型会较亮，边缘不会有阴影感，整个材质球更加平，但其峰值相比于观察数据，不够强。并且对于粗糙材质，颜色表现得过于平。
  • Hanrahan-Krueger Model
    Hanrahan-Krueger Model 同样也预测到 retroreflective peak，并且 grazing 角度相较于 Oren-Nayar 模型会更亮，并且其颜色过渡非常平滑。但在观察的数据中，颜色与光强度会在 $\theta_l/\theta_v$ 等值线上具有变化。

2.1.3 较为精确的经验模型

根据观察结论，Disney 开了一种漫反射的经验模型，该模型可以在光滑表面的 Fresnel 阴影与粗糙表面的亮度增加之间过渡。并且该模型的 Fresnel Factor 采用了一种遵循 Helmholtz reciprocity 性质的形式，即互换入射与出射(观察)方向，结果不变。此外 Fresnel Factor 采用 Schlick 近似，即入射角为 $\theta$ 的 Fresnel 反射率：
$$
F_R \approx F(\theta)=F_0+(1-F_0)(1-\cos\theta)^5
$$
其中 $F_0$ 与折射前后的介质的折射率有关，$F_0=\left(\frac{\eta_1-\eta_2}{\eta_1+\eta_2}\right)^2$ 。

Disney 的diffuse 经验模型为：
$$
f_d = \frac{baseColor}{\pi}\cdot\left(1+(F_{D90}-1)(1-\cos\theta_l)^5\right)\cdot\left(1+(F_{D90}-1)(1-\cos\theta_v)^5\right) \tag{2} \label{Diffuse Model}
$$
其中，$F_{D90}=0.5+2\cdot roughness \cdot \cos^2\theta_d$ ，$\theta_d$ 为入射与出射方向的夹角的一半。可以看出该模型满足互换入射与出射方向，结果相同。从公式中可以看出，越往 grazing retroreflection 偏移，即 $\theta_l$ 与 $\theta_v$ 向 $90$ 偏移，次幂项系数越大，对应了 grazing retroreflection 处的峰值，并且 $F_{D90}$ 与 roughness 相关，越粗糙越大，对应了粗糙表面，漫反射会更亮。

Disney 对上式的实现代码

1
2
3
4
5
6
7
// [Burley 2012, "Physically-Based Shading at Disney"]
float3 Diffuse_Burley_Disney( float3 DiffuseColor, float Roughness, float NoV, float NoL, float VoH ){
	float FD90 = 0.5 + 2 * VoH * VoH * Roughness;
	float FdV = 1 + (FD90 - 1) * Pow5( 1 - NoV );
	float FdL = 1 + (FD90 - 1) * Pow5( 1 - NoL );
	return DiffuseColor * ( (1 / PI) * FdV * FdL );
}

2.2 Specular D

当前的微表面法线分布函数的 specular lobe 不够长，GGX 具有比其他法线分布函数更长的尾部，但仍然无法捕捉到 chrome sample 中高光附近的余晖。如下图所示

image-20211229135245256
左图为 chrome(黑)、GGX(红)、Benckmann(绿) 的镜面反射随 $\theta_h$ 变化的曲线； 右图分别为 chrome、GGX、Beckmann 对点光源的响应

在流行的模型中，GGX(Trowbridge-Reitz) 具有最长的尾部，但很多材质需要更长的尾部。

2.2.1 GTR 分布函数

GTR 根据 Berry 和 GGX(TR) 分布函数的相似之处，而推广得到的广义形式。GTR 参数化分母的次幂，调整尾部的长度。Berry、TR 、GTR 微表面法线分布函数的形式如下：
$$
\begin{align}
D_{Berry}&=\frac{c}{(\alpha^2\cos^2\theta_h+\sin^2\theta_h)} \
D_{TR}&=\frac{c}{(\alpha^2\cos^2\theta_h+\sin^2\theta_h)^2} \
D_{GTR}&=\frac{c}{(\alpha^2\cos^2\theta_h+\sin^2\theta_h)^\gamma}
\end{align}
$$
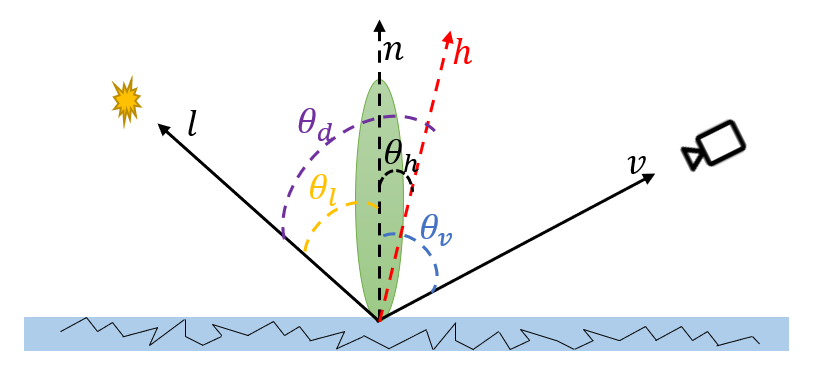
其中，$c$ 为缩放常数；$\alpha$ 为 roughness；$\theta_h$ 为入射方向与观察方向的 half vector，与法线该 half vector 一致的微表面才可能将入射光反射到观察方向，因此分布函数得到这个方向上的微表面法线的重要程度，从而知道宏表面的微表面集合有多少比例可以贡献到观察方向上；$\gamma$ 可以调整 BRDF lobe 的长度，越大越长，如下图所示

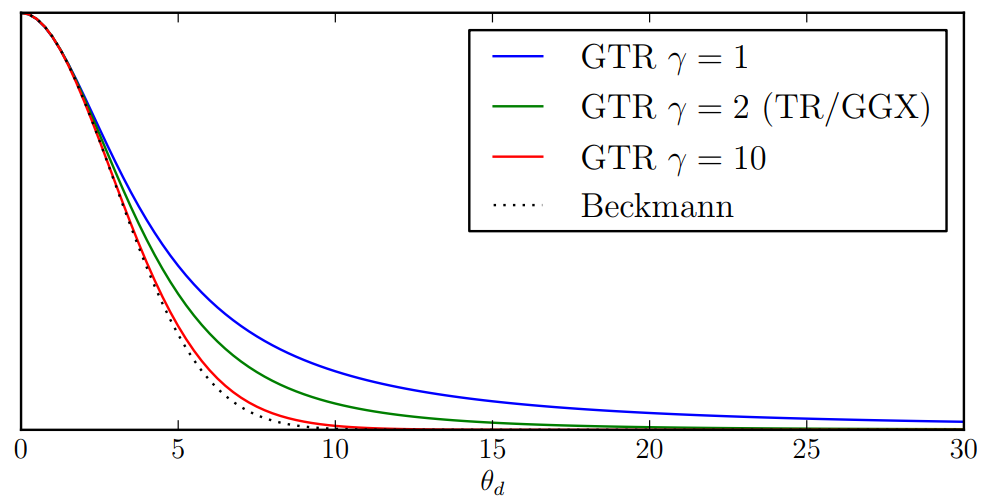
image-20211229151526527

Disney 设计的 BRDF 具有两个 GTR BRDF lobe：

  • Primary lobe：$\gamma = 2$，表示基础底材质，可以是各向同性/各向异性的金属或非金属。
  • Secondary lobe：$\gamma = 1$，表示基础材质层上的 clearcoat layer(清漆层)，一般为各向同性的非金属。

友好的参数调控交互处理：

  • 重新定义公式中的 $\alpha$：$\alpha = roughness^2$ 的变化更加线性，因此 UI 调参时，调整的是 $\alpha^{1/2}$。

各向同性的 GTR 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Generalized-Trowbridge-Reitz distribution
float D_GTR1(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return (a2 - 1.0) / (PI * log(a2) * den);
}

float D_GTR2(float alpha, float dotNH)
{
    float a2 = alpha * alpha;
    float cos2th = dotNH * dotNH;
    float den = (1.0 + (a2 - 1.0) * cos2th);

    return a2 / (PI * den * den);
}

各向异性的 GTR 代码

1
2
3
4
5
float D_GTR2_aniso(float dotHX, float dotHY, float dotNH, float ax, float ay)
{
    float deno = dotHX * dotHX / (ax * ax) + dotHY * dotHY / (ay * ay) + dotNH * dotNH;
    return 1.0 / (PI * ax * ay * deno * deno);
}

2.2.2 Specular F

Disney 直接使用 Schlick 近似代替 Fresnel equation：
$$
F_{Schlick}=F_0+(1-F_0)(1-\cos\theta_d)^5
$$
其中，常数 $F_0$ 表示垂直入射时的镜面反射率，$\theta_d$ 表示入射光与微表面法线(入射方向与观察方向的 half vector)的夹角。

Schlick Fresnel 的 shader 代码

1
2
3
4
5
// [Schlick 1994, "An Inexpensive BRDF Model for Physically-Based Rendering"]
float3 F_Schlick(float HdotV, float3 F0)
{
    return F0 + (1 - F0) * pow(1 - HdotV , 5.0));
}

另外，Disney 在 SIGGRAPH 2015 提出在介质间相对IOR接近1时，Schlick近似误差较大，这时采用精确的菲涅尔方程。

2.3 Specular G

参数设计

  • baseColor：表面颜色，通常由纹理贴图提供。

  • subsurface（次表面）：漫反射向次表面散射的靠拢程度。

  • metallic（金属度）：0 = 电介质（绝缘体），1 =金属。这是两种不同模型之间的线性混合。金属模型没有漫反射成分，并且还具有等于基础色的着色入射镜面反射。

  • specular（镜面反射强度）：入射镜面反射量。用于取代折射率。

  • specularTint（镜面反射颜色）：对美术控制的让步，用于对基础色（basecolor）的入射镜面反射进行颜色控制。掠射镜面反射仍然是非彩色的。

  • roughness（粗糙度）：表面粗糙度，控制漫反射和镜面反射。

  • anisotropic（各向异性强度）：各向异性程度。用于控制镜面反射高光的纵横比。（0 =各向同性，1 =最大各向异性。）

  • sheen（光泽度）：一种额外的掠射分量（grazing component），主要用于布料。

  • sheenTint（光泽颜色）：对sheen（光泽度）的颜色控制。

  • clearcoat（清漆强度）：有特殊用途的第二个镜面波瓣（specular lobe）。

  • clearcoatGloss（清漆光泽度）：控制透明涂层光泽度，0 = “缎面（satin）”外观，1 = “光泽（gloss）”外观。

以上参数取值都为 $[0,1]$。

Reference

[1] Burley B, Studios W D A. Physically-based shading at disney[C] ACM SIGGRAPH. 2012, 2012: 1-7.

[2] https://zhuanlan.zhihu.com/p/60977923

Rendering Blogs > Graphics > PBR
Disney BRDF
http://example.com/2024/10/14/Rendering Blogs/Graphics Basis/Disney Principled BRDF/
Author
John Doe
Posted on
October 14, 2024
Licensed under