PBR Material

1 Summary

2 Microfacet BRDF

微表面模型认为宏观表面的着色区域上分布着很多微表面，不同材质具有不同的微表面法线分布。如集中的微表面法线分布对应 glossy 材质，反之分散的分布对应 diffuse 材质。有如下表面及入射光、视角，

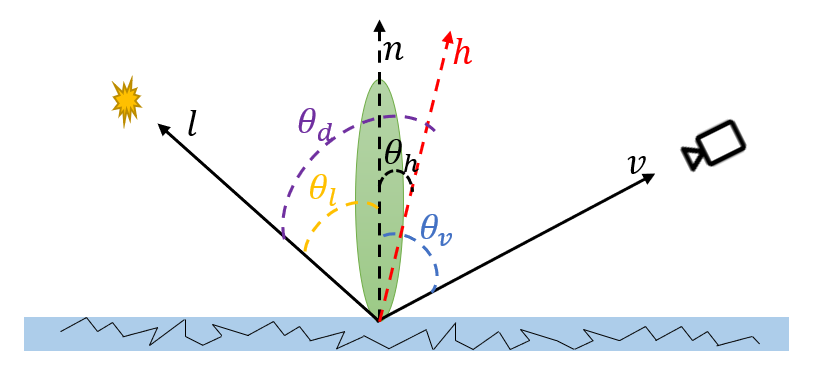
入射光方向 $\boldsymbol{l}$、观察方向 $\boldsymbol{v}$、宏观表面法向量 $\boldsymbol{n}$、half vector $\boldsymbol{h}=\frac{\boldsymbol{l}+\boldsymbol{v}}{||\boldsymbol{l}+\boldsymbol{v}||}$；$\boldsymbol{l}$ 与 $\boldsymbol{n}$ 夹角为 $\theta_l$，$\boldsymbol{v}$ 与 $\boldsymbol{n}$ 的夹角为 $\theta_v$，$\boldsymbol{h}$ 与 $\boldsymbol{n}$ 的夹角为 $\theta_h$，$\boldsymbol{l}$ 与 $\boldsymbol{h}$ 的夹角等于 $\boldsymbol{v}$ 与 $\boldsymbol{h}$ 的夹角为 $\theta_d$。微表面 BRDF 定义为：
$$
\begin{align}
f(\boldsymbol{l},\boldsymbol{v})&=\frac{F(\boldsymbol{l},\boldsymbol{v})\cdot G(\boldsymbol{l},\boldsymbol{v},\boldsymbol{h})\cdot D(\boldsymbol{h})}{4(\boldsymbol{n}\cdot \boldsymbol{l})(\boldsymbol{n}\cdot \boldsymbol{v})} \
&=\frac{F(\theta_d)\cdot G(\theta_l, \theta_v)\cdot D(\theta_h)}{4\cdot \cos\theta_l\cdot \cos\theta_v}
\end{align}
$$
Microfacet BRDF 有三个重要成分，

Fresnel term : $F(\theta_d)$，反射率，即给定入射方向，在观察方向上有多少能量会被反射。
NDF(distribution of normal) : $D(\theta_h)$，微表面的法线分布。
Shadow-Masking term : $G(\theta_l,\theta_v)$，微表面产生的自遮挡。

除此之外，分母中的 $4\cdot \cos\theta_l\cdot \cos\theta_v$ 是微表面 BRDF 推导得到。

2.1 Fresnel term (Specular F) [1]

入射光在物体表面可能会发生反射、折射或两者都会发生，Fresnel term 则用来描述物体反射或折射入射能量的多少。

2.1.1 Reflection

只考虑反射，即入射光打到镜面。如下图所示

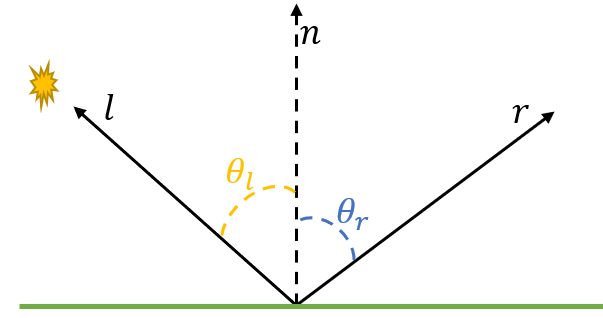
入射光 $\boldsymbol{l}$、反射光方向 $\boldsymbol{r}$、法线方向 $\boldsymbol{n}$，入射光与法线夹角 $\theta_l$ 、发射光与法线夹角 $\theta_r$，由反射定律可知 $\theta_l$ 与 $\theta_r$ 相等。已知入射光线、法线，可以求得反射光线：
$$
\boldsymbol{r}=2\cdot (\boldsymbol{n}\cdot \boldsymbol{l}) \boldsymbol{n} - \boldsymbol{l}
$$

这个反射公式可以由简单的几何推导得到，$\boldsymbol{l}$ 与 $\boldsymbol{r}$ 的夹角被 $\boldsymbol{n}$ 均分，并且由于是方向向量长度都为 1，因此可做菱形

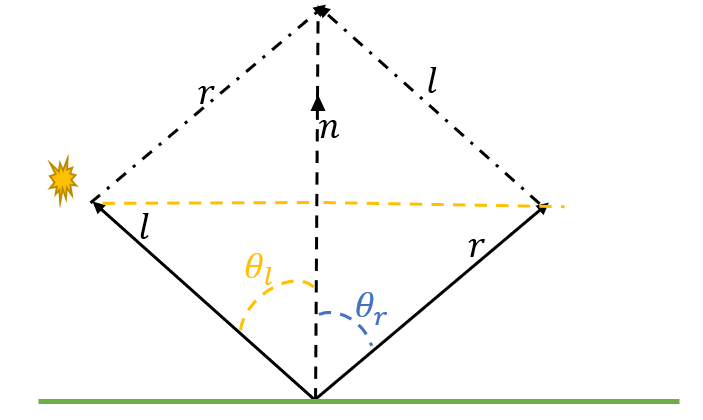
其中 $\boldsymbol{n}$ 所在对角线长度为 $2\cdot ||\boldsymbol{l}||\cdot \cos\theta_l=2\cdot \cos\theta_l$，对角线向量为 $2\cdot cos\theta_l \cdot \boldsymbol{n}$，因此反射向量
$$
\boldsymbol{r} = 2\cdot \cos\theta_l\cdot \boldsymbol{n} - \boldsymbol{l}=2\cdot (\boldsymbol{n}\cdot \boldsymbol{l}) \boldsymbol{n} - \boldsymbol{l}
$$
如果将入射光方向写为光源指向交点形式，那么反射向量为
$$
\boldsymbol{r}= \boldsymbol{l} - 2\cdot (\boldsymbol{n}\cdot \boldsymbol{l}) \boldsymbol{n}
$$

对于单条入射光，只有观察方向与反射方向重合，才能看到反射的入射光与物体交点信息。如波光粼粼的效果

![image-20211226133750761](/images/Rendering Blogs/Graphics Basis/Real-Time Physically Based Material Basics.assets/image-20211226133750761.png)

2.1.2 Refraction (transmission)

对于具有透明性质的物体，光接触时会有折射发生，即光会传播至物体内部。折射光的方向与传输介质的折射率有关 (index of refraction、ior)。折射率定义为 $\eta = \frac{c}{v}$，其中 $c$ 为光在真空中的传播速度，$v$ 为光在传播介质中的传播速度。

折射定律 (snell’s law)：已知入射光 $\boldsymbol{l}$，法线 $\boldsymbol{n}$，入射角 $\theta_1$，光折射前后的传播介质的折射率分别为 $\eta_1$、$\eta_2$，光接触到表面发生折射得到折射角为 $\theta_2$ 的 transmissive ray $\boldsymbol{t}$，有
$$
\frac{\sin\theta_1}{\sin\theta_2} = \frac{\eta_2}{\eta_1}
$$
如下图所示：

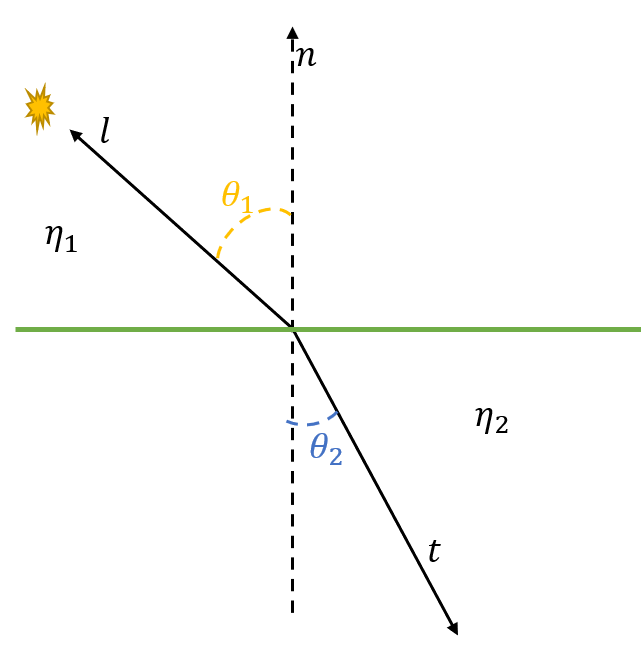
求解 transmissive ray $\boldsymbol{t}$ 有：

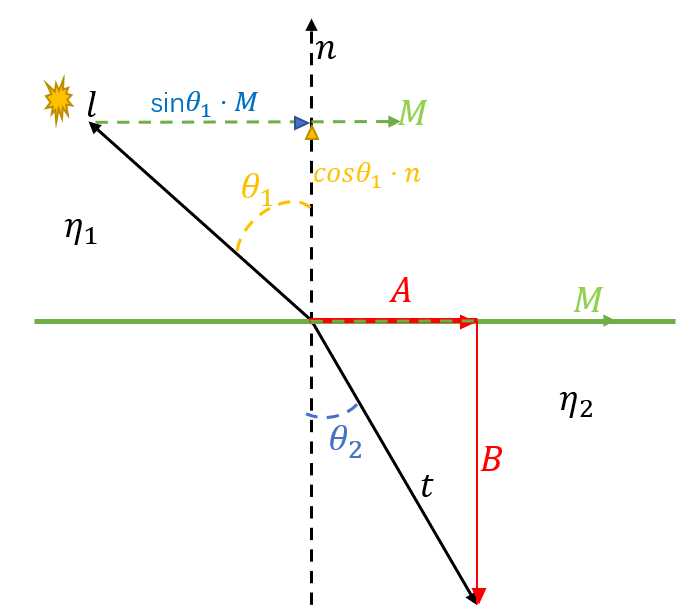
如上图所示，入射光与物体的交点处切向量为 $M$，transmissive ray $\boldsymbol{t}$ 在切线方向与法线方向的分量分别为 $A,B$，因此有
$$
\begin{align}
\boldsymbol{t} &= A+B \
A &= ||\boldsymbol{t}|| \cdot \sin\theta_2 \cdot M = \sin\theta_2 \cdot M \
B &= ||\boldsymbol{t}|| \cdot \cos\theta_2 \cdot -\boldsymbol{n} = \cos\theta_2 \cdot -\boldsymbol{n} \
\boldsymbol{t} &= \sin\theta_2 \cdot M - \cos\theta_2 \cdot \boldsymbol{n}
\end{align}
$$

求交点处的切向量
$$
\begin{align}
& ||M|| \cdot \sin\theta_1 \cdot M=\cos\theta_1\cdot \boldsymbol{n}-\boldsymbol{l} \
& M = \frac{\cos\theta_1\cdot \boldsymbol{n}-\boldsymbol{l}}{\sin\theta_1}
\end{align}
$$
由折射定律求 $\theta_2$
$$
\begin{align}
\sin\theta_2 &= \frac{\eta_1}{\eta_2}\cdot \sin\theta_1\
\cos\theta_2 &= \sqrt{1-\sin^2\theta_2}=\sqrt{1-\frac{\eta_1^2}{\eta_2^2}\cdot \sin^2\theta_1}
\end{align}
$$

最终有：
$$
\boldsymbol{t} = \frac{\eta_1}{\eta_2}\cdot (\cos\theta_1\cdot \boldsymbol{n}-\boldsymbol{l})-\sqrt{1-\frac{\eta_1^2}{\eta_2^2}\cdot \sin^2\theta_1}\cdot \boldsymbol{n}
$$
令
$$
\begin{align}
\eta &= \frac{\eta_1}{\eta_2}\
c_1 &= \cos\theta_1=\boldsymbol{l}\cdot\boldsymbol{n}\
c_2 &= \sqrt{1-\frac{\eta_1^2}{\eta_2^2}\cdot \sin^2\theta_1} = \sqrt{1-\eta^2\cdot(1-c_1^2)}
\end{align}
$$
有，
$$
\begin{align}
\boldsymbol{t}&=\eta \cdot (c_1\cdot\boldsymbol{n}-\boldsymbol{l})-c_2\cdot \boldsymbol{n} \
&=(\eta\cdot c_1-c_2)\cdot \boldsymbol{n}-\eta\cdot\boldsymbol{l}
\end{align}
$$

如果入射光方向写为指向交点的形式，上述推导需要些许修改

交点处切向量
$$
\begin{align}
& ||M|| \cdot \sin\theta_1 \cdot M=\boldsymbol{l} + \cos\theta_1\cdot \boldsymbol{n} \
& M = \frac{\boldsymbol{l} + \cos\theta_1\cdot \boldsymbol{n}}{\sin\theta_1}
\end{align}
$$

参数定义

$$
c_1=\cos\theta_1=-\cos(\pi-\theta_1)=-\boldsymbol{l}\cdot\boldsymbol{n}
$$

折射光为
$$
\begin{align}
\boldsymbol{t} &= \eta\cdot(\boldsymbol{l} + c_1\cdot \boldsymbol{n})-c_2\cdot \boldsymbol{n} \
&= (\eta\cdot c_1-c_2)\cdot \boldsymbol{n}+\eta\cdot\boldsymbol{l}
\end{align}
$$

2.1.3 Fresnel

Fresnel 用来描述物体反射入射光的多少、折射入射光的多少，其精确的数学模型为 Fresnel equation。Fresnel equation 将入射光分解为一组互相垂直的波，即平行偏振（p 极化）光，位于入射光、反射光与折射光组成的平面内；垂直偏振（s 极化）光，垂直于入射光、反射光与折射光组成的平面。p 极化入射光与 s 极化入射光的反射比（反射光能量占入射光能量的比例）分别为，
$$
F_{R_{||}}=\left(\frac{\eta_2\cos\theta_1-\eta_1\cos\theta_2}{\eta_2\cos\theta_1+\eta_1\cos\theta_2}\right)^2 \
F_{R_{\perp}}=\left(\frac{\eta_1\cos\theta_2-\eta_2\cos\theta_1}{\eta_1\cos\theta_2+\eta_2\cos\theta_1}\right)^2
$$
其中，$\eta_1,\eta_2$ 分别为折射前后的介质的折射率(ior)，$\theta_1$ 为入射角，$\theta_2$ 为折射角。特殊地，图形学中通常考虑无偏振入射光，即含有等量的 s 极化与 p 极化，反射比为，
$$
F_R=\frac{1}{2}(F_{R_{||}}+F_{R_{\perp}})
$$
无论入射光是否有偏振，根据能量守恒，透射比（折射光能量占入射光能量的比例）都为，
$$
F_T=1-F_R
$$
下面两图为 s 极化、p 极化以及无极化的入射光条件下，不同入射角度的反射比曲线图，左图为绝缘体（Dielectric，$\eta=1.5$），右图为导体

左图为绝缘体反射比曲线，右图为导体反射比曲线

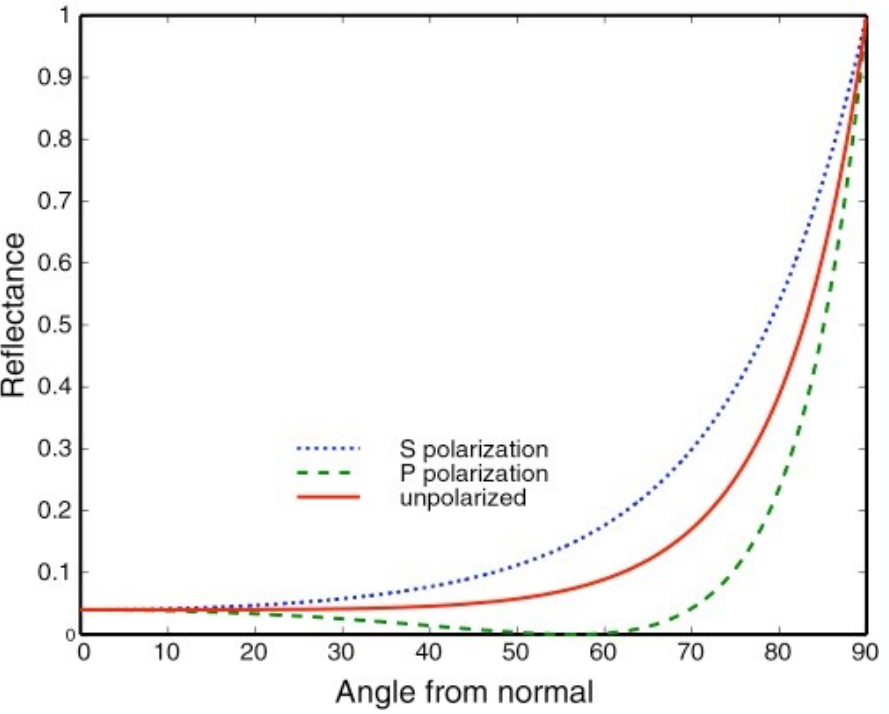
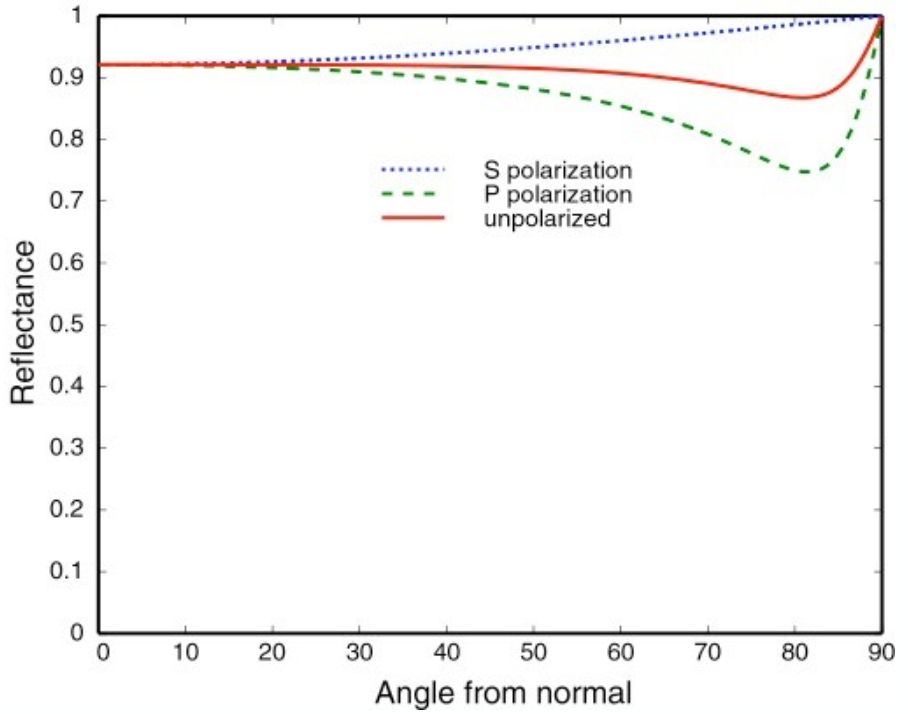
Schlick’s Approximation

精确的 Fresnel equation 计算非常复杂，通常使用其近似形式——Schlick’s 近似。
$$
\begin{align}
F_R\approx F_{Schlick}&=F_0+(1-F_0)(1-\cos\theta)^5 \
&=(1-\cos\theta)^5\cdot 1 + (1-(1-\cos\theta)^5)\cdot F_0\
where \quad F_0=&\left(\frac{\eta_1-\eta_2}{\eta_1+\eta_2}\right)^2,\cos\theta=\boldsymbol{l}\cdot\boldsymbol{h}
\end{align}
$$

$F_0$ 是沿着法线方向垂直入射时的反射率，当入射方向与法线夹角越来越大时，反射率也随之增大，直至入射方向与法线呈 $90^\circ$ 达到最大，由上式可知，此时为 $1$。上式的含义就是在垂直入射反射率与 grazing 入射反射率(白光) 之间的插值，角度越接近 $90^\circ$，反射率越接近白光。

2.2 NDF (Specular D)

NDF(Normal Distribution Function) 为微表面法线分布函数，描述微观表面的微表面法线的统计分布。着色时，我们需要得到观察方向能够看到的信息，并且当入射光方向和观察方向的 half vector 与法线重合时，对应信息才能被观察到。因此我们需要得到微表面法线在此 half vector 方向上的分布情况，即概率。 NDF 输入某点的 roughness(微表面法线集中程度，越集中 roughness 越低)、宏观表面法线以及入射光方向与观察方向的 half vector 作为微表面法线方向，输出分布函数在此微表面法线方向的概率。

[2] 这篇博客总结得很好，不再赘述

2.3 Shadow-Masking Term (Specular G)

[3] 这篇博客总结得很好，不再赘述

3 Diffuse BRDF

3.1 Lambertian Diffuse BRDF

Lambertian 模型将漫发射理解为：光交于 diffuse 表面发生折射，在物体表面下进行了充足的散射后离开表面，向每个方向均匀反射，因此 Lambertian Diffuse BRDF 是一个常数。假设该常数为 $\mathcal{C}$，下面根据能量守恒推算出 $\mathcal{C}$。我们先来介绍 Lambert’s Consine Law。

3.1.1 Lambert’s Cosine Law

对于以一定角度入射的 irradiance，物体接受到的 irradiance 与角度余弦成正比，该角度为入射方向与法线的夹角。详情查看 [4] 的 Irradiance(辐照度)部分。

3.1.2 能量守恒计算 Lambertian Diffuse BRDF

假设空间中任何方向入射的光 radiance 都一样，即 unifom incident lighting。如果物体不吸收光，根据能量守恒，入射 irradiance 等于出射 irradiance。假设入射方向 $\omega_i$ 的入射 irradiance 为 $L_i(\omega_i)$，入射角为 $\theta_i$，那么在 $\omega_o$ 出射方向上的出射 irradiance 为，
$$
L_o(\omega_o)=\int_{\Omega^+} \mathcal{C}\cdot L_i(\omega_i)\cdot \cos\theta_i\space d\omega_i
$$
由于是 uniform incident lighting，因此入射 irradiance 是常数，上式可变为，
$$
\begin{align}
L_o(\omega_o)&=\mathcal{C}\cdot L_i\cdot\int_{\Omega^+}\cos\theta_i\space d\omega_i \
&= \mathcal{C}\cdot L_i\cdot\int_0^{2\pi}\int_0^{\pi/2}\cos\theta_i\sin\theta_i\space d\theta_id\phi_i \
&= \mathcal{C}\cdot L_i\cdot\pi
\end{align}
$$
由于 Lambertian 模型认为每个方向均匀反射，因此 $L_o$ 是常数，所以有 $L_o=L_i$，Lambertian Diffuse BRDF (无能量损失情况下)为
$$
\mathcal{C}=\frac{1}{\pi}
$$

3.1.3 具有能量损失的 diffuse 材质

上述为了计算出 diffuse brdf 假定了无能量损失，但大多数材质会有能量吸收，只有部分能量反射出。反射能量的多少即为反射率，听起来像是前述 Fresnel 的功能，但并非如此。Fresnel 是定义在无限小且无限光滑的微表面上的，例如前述的反射定律与折射定律的计算过程。而 Lambertian diffuse 材质是针对整个宏表面，在整个宏表面上均匀反射，因此 diffuse 材质的反射率不需要 Fresnel 这样精确的微观尺度。

实际中的 Lambertian diffuse 材质的反射率是通过 albedo 来定义，albedo 一般又定义为 diffuse color。这也符合我们常识中对颜色的认知——颜色即物体吸收了入射光的部分波段而反射出剩余波段的能量。diffuse color 在图形学中视为物体的固有色，即在自然界日光照射下所呈现的颜色。

因此，在具有能量损失时，Lambertian Diffuse BRDF 为
$$
f_{diffuse}=\frac{albedo}{\pi}=\frac{C_{diffuse}}{\pi}
$$