3.1 Ray-Triangle and Ray-bounding box Intersection

1 Preliminary

1.1 定义光线

光线起点(position) $O$, 方向 $\textbf{d}$ (eye到所着色像素的方向)。由此可得到下面光线方程(Ray equation)，该式定义的是光线上的任一点。
$$
r(t)=O+t\textbf{d}, \quad 0\leq t\leq \infty \label{ray-equation} \tag{1}
$$

1.2 叉乘

给定两个向量 $\mathbf{a}=(\mathbf{a}_x,\mathbf{a}_y,\mathbf{a}_z)$，$\mathbf{b}=(\mathbf{b}_x,\mathbf{b}_y,\mathbf{b}_z)$，叉乘公式为

$$
\begin{align*} \mathbf{a}\times \mathbf{b}&=\begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \ \mathbf{a}_x & \mathbf{a}_y & \mathbf{a}_z \ \mathbf{b}_x &\mathbf{b}_y&\mathbf{b}_z\end{vmatrix}= \begin{vmatrix}\mathbf{a}_y&\mathbf{a}_z \ \mathbf{b}_y&\mathbf{b}_z\end{vmatrix}\mathbf{i}+\begin{vmatrix}\mathbf{a}_x&\mathbf{a}_z \ \mathbf{b}_x&\mathbf{b}_z\end{vmatrix}\mathbf{j}+\begin{vmatrix}\mathbf{a}_x&\mathbf{a}_y \ \mathbf{b}_x&\mathbf{b}_y\end{vmatrix}\mathbf{k}\ &=(\mathbf{a}_y\mathbf{b}_z-\mathbf{a}_z\mathbf{b}_y)\mathbf{i}+(\mathbf{a}_x\mathbf{b}_z-\mathbf{a}_z\mathbf{b}_x)\mathbf{j}+(\mathbf{a}_x\mathbf{b}_y-\mathbf{a}_y\mathbf{b}_x)\mathbf{k}\end{align*} \label{cross-product} \tag{2}
$$
可以看出，$\mathbf{i},\mathbf{j},\mathbf{k}$ 三个方向的符号由其他两个方向对应的行列式确定。

叉乘也可用于求三角形面积

• $\frac{1}{2}||\mathbf{a}\times \mathbf{b}||=\frac{1}{2}||\mathbf{a}||\cdot ||\mathbf{b}||sin\theta$，其中 $||\mathbf{b}||sin\theta$ 为 $\mathbf{a}$ 对应的边上的高。因此叉乘得到的向量的模的一半为三角形面积。

• 对于二维平面上的三角形，只需给每个顶点加上一个相同的第三个坐标，假设为 $0$，带入叉乘公式有$\mathbf{a}\times\mathbf{b}=0\cdot\mathbf{i}+0\cdot\mathbf{j}+(\mathbf{a}_x\mathbf{b}_y-\mathbf{a}_y\mathbf{b}_x)\cdot\mathbf{k}=(0,0,\mathbf{a}_x\mathbf{b}_y-\mathbf{a}_y\mathbf{b}_x)$，那么三角形面积

  $\frac{1}{2}||\mathbf{a}\times\mathbf{b}||=\frac{1}{2}|\mathbf{a}_x\mathbf{b}_y-\mathbf{a}_y\mathbf{b}_x|$

1.3 重心坐标(Barycentric Coordinates)

重心坐标是三角形的一个坐标系统，常用于三角形内部插值。简单来说，三角形内部任意一点都可以使用重心坐标 $(\alpha,\beta,\gamma)$ 描述，假设三角形三个顶点为 $A,B,C$，三角形内部一点 $S=\alpha A+\beta B+\gamma C$，其中 $\alpha+\beta+\gamma=1$。

重心坐标求解，如下图所示 $A_A,A_B,A_C$ 分别为划分的三个小三角形面积，重心坐标为

$$\begin{cases} \alpha=\frac{A_A}{A_A+A_B+A_C} \ \beta=\frac{A_B}{A_A+A_B+A_C} \ \gamma=\frac{A_C}{A_A+A_B+A_C} \end{cases}$$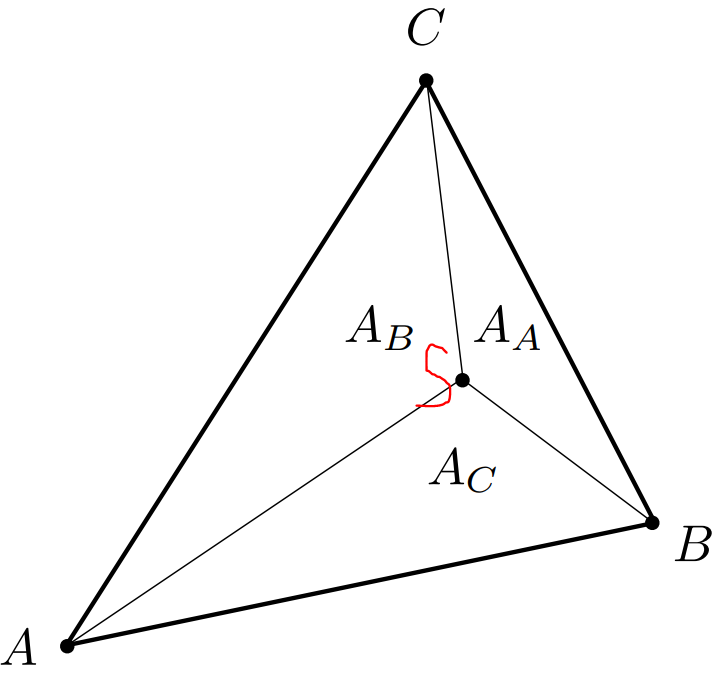

使用叉乘计算面积，有 $\begin{cases}A_A=\frac{1}{2}||\mathbf{SC}\times \mathbf{SB}|| \ A_B=\frac{1}{2}||\mathbf{SC}\times \mathbf{SA}|| \ A_C=\frac{1}{2}||\mathbf{SA}\times \mathbf{SB}||\end{cases}$

这里的重心坐标定义方式， $\alpha,\beta,\gamma$ 都为 $[0,1]$ 之内时，证明点 $S$ 位于三角内。

一般使用简化方法，查看 Watertight Ray-Triangle Intersection 部分定义

**重心坐标具有仿射不变性，即仿射变换前后重心坐标不变。**仿射变换是一个线性变换(旋转、缩放、切变等)加上一个平移变换，变换前后的坐标维度不变。透视投影属于非线性变换，重心坐标会发生改变。因此，三维空间得到的重心坐标不能用于透视投影的 clip 空间，反之亦然。

2 光线与三角形求交点

2.1 Moller Trumbove Algorithm

使用重心坐标 $(1-b1-b2,b1,b2)$ 表示交点，与光线方程联立方程组可列，

$$
O+t\textbf{d}=(1-b_1-b_2)P_0+b_1P_1+b_2P_2
$$
使用线性代数中的克拉姆法则可得

$$
\begin{pmatrix} t \ b_1\b_2 \end{pmatrix}=\frac{1}{\mathbf{S_1}\cdot\mathbf{E_1}}\begin{pmatrix}\mathbf{S_2}\cdot \mathbf{E_2} \ \mathbf{S_1}\cdot \mathbf{S} \ \mathbf{S_2}\cdot \mathbf{d}\end{pmatrix}, \quad \mathrm{where}\space\begin{cases} \mathbf{E_1} = P_1-P_0 \ \mathbf{E_2} = P_2-P_0 \ \mathbf{S}=O-P_0 \ \mathbf{S_1}=\mathbf{d} \times \mathbf{E_2} \ \mathbf{S_2}=\mathbf{S} \times \mathbf{E_1} \end{cases}
$$
如果 $t, b_1,b_2,1-b_1-b_2$都非负，则证明交点在三角形内。

2.2 Watertight Ray-Triangle Intersection

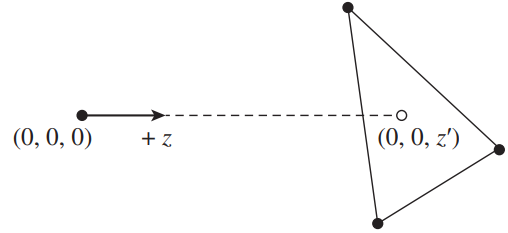
Key idea: 构建一个以光线起点为原点，以光线方向为 $z$ 轴正方向的坐标系。将三角形变换到该坐标系，在该坐标系中进行求交。由于光线为 $z$ 轴，因此，若有交点，则交点 $x,y$ 坐标必为 $0$。反之，如果三角形内部有一点 $x,y$ 坐标为 $0$ ，且该点在光线范围内，那么此点必为交点。

因此，三维空间的求交问题，降为了二维空间问题。我们忽略三角形顶点的 $z$ 坐标，判断 $(0,0)$ 点是否在三角形内部即可。

2.2.1 构建 ray coordinate system

（1）平移光线起点至原点
$$
\mathbf{T}=\begin{pmatrix} 1&0&0&-O_x \ 0&1&0&-O_y \ 0&0&1&-O_z \ 0&0&0&1 \end{pmatrix}
$$
（2）将 ray 方向尺度最大的维度作为到 $z$ 轴

将 ray 方向绝对值最大的维度变换到 $z$ 维度上，其他两个维度的顺序任意。这一步确保了，ray 方向 $z$ 维度不为 $0$。

假设 ray 方向绝对值最大的维度为 $x$，那么进行 $x,z$ 互换，得到如下 permutation 变换。此矩阵不唯一，只要将最大的维度变换到 $z$ 维度即可。

$$
\mathbf{P}=\begin{pmatrix} 0&0&1&0 \ 0&1&0&0 \ 1&0&0&0 \ 0&0&0&1 \end{pmatrix}
$$
（3）使用切变将 ray 方向变换到 $z$ 轴正向

此过程不使用旋转，而使用效率更高的切变。切变(shear)变换：
$$
\mathbf{S}=\begin{pmatrix} 1&0&-\mathbf{d}_x/\mathbf{d}_z&0 \ 0&1&-\mathbf{d}_y/\mathbf{d}_z&0 \ 0&0&1/\mathbf{d}_z &0\ 0&0&0&1 \end{pmatrix}
$$

将 $\mathbf{d}=(\mathbf{d}_x,\mathbf{d}_y,\mathbf{d}_z,0)$ 代入切变有 $\mathbf{S}\mathbf{d}=(0, 0, 1,0)$，即把 ray 方向变换为 $z$ 轴正向。

至此完成了到 ray coordinate system 的变换 $\mathbf{SPT}$，通过该变换即可将三角形的顶点变换到 ray coordinate system。例如三角形顶点 $p$，有 $\mathbf{SPT}p$

注意 $\mathbf{SPT}$ 只与光线有关，因此可在光线生成时构建出来，而不需要每次求交都构建一次。

2.2.2 求交点

经过第 (1) 步的变换，求交问题转为了判断 $(0,0)$ 是否在三角形内。如下图所示

Fig-1：ray coordinate system 下的三角形

（1）判断点是否在三角形内部

• 三维空间下的做法。
  点在三角形内部的前提是，点必须和三角形共面。只考虑平面上一个三角形和一点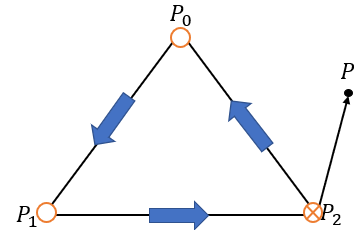 以一定顺序定义三角形顶点组成的向量，如图中 $P_0P_1P_2$ 顺序，有向量 $P_0P_1$、$P_1P_2$、$P_2P_0$，平面上一点 $P$ ，得到向量 $P_0P$、$P_1P$、$P_2P$ 。 判断点 $P$ 是否在三角形内。如果 $P_0P_1\times P_0P$、$P_1P_2\times P_1P$、$P_2P_0\times P_2P$ 三个向量的方向相同，则 $P$ 位于三角形内部。图中 $\circ$、$\otimes$ 分别表示叉乘方向向外和向内，因此可得到图中 $P$ 点不在三角形内。

如果直接应用上述方法，那么计算仍会涉及三维坐标，ray coordinate 坐标系的转换就没有意义。这里我们简化一下问题，考虑 Fig-1 所示情况。我们所关注的叉乘方向有两种，一种位于三角形的左侧，一种位于三角形的右侧。使用叉乘向量 $z$ 坐标的符号来区分这两种情况。

由叉乘 $\eqref{cross-product}$ 可知，$(\mathbf{a}x\mathbf{b}y-\mathbf{a}y\mathbf{b}x)$ 决定叉乘方向 $z$ 坐标的符号，其中 $\mathbf{a},\mathbf{b}$ 分别为参与叉乘的第一和第二个向量。因此，我们只需要 $x,y$ 两个坐标即可判断点是否在三角形内。$(\mathbf{a}x\mathbf{b}y-\mathbf{a}y\mathbf{b}x)$ 也称为 signed edge function：
$$
\begin{cases} e_0(P)=(P{1x}-P{0x})(P_y-P{0y})-(P{1y}-P{0y})(P_x-P{0x}) \ e_1(P)=(P{2x}-P{1x})(P_y-P_{1y})-(P_{2y}-P_{1y})(P_x-P_{1x}) \ e_2(P)=(P_{0x}-P_{2x})(P_y-P_{2y})-(P_{0y}-P_{2y})(P_x-P_{2x})\end{cases}
$$
如果 $e_0(P),e_1(P),e_2(P)$ 三者符号相同，那么证明 $P$ 点位于三角形内部。当三角形与光线方向平行，即三角形法线垂直于 $z$ 轴时，$e_0,e_1,e_2$ 都为 $0$ ，此时忽略。其他情况，$e_0,e_1,e_2$ 都不应为 $0$，但可能由于浮点精度而为 $0$，此时无法判断 $P$ 点是否在三角形内部。

由于第 (1) 步的特殊处理，只需要判断 $(0,0)$ 点是否位于三角形内，即 $P=(0,0)$，带入 signed edge function 有，

$$
\begin{cases} e_0(P)= P_{0x}P_{1y}-P_{0y}P_{1x} \ e_1(P)=P_{1x}P_{2y}-P_{1y}P_{2x} \ e_2(P)=P_{2x}P_{0y}-P_{2y}P_{0x}\end{cases}
$$
如果 $e_0,e_1,e_2$ 同号，则证明 $P=(0,0)$ 点位于三角形内。

（2）计算交点

求解交点，即求光线方程参数 $t$。由于 ray coordinate system 的特性，光线为 $z$ 轴，且指向 $z$ 轴正向，交点的 $z$ 坐标即为参数 $t$。

继续看叉乘的另一个性质，叉乘向量的模的一半为两个参与叉乘的向量组成的三角形的面积，再看重心坐标的公式定义。

因此 $P=(0,0)$ 的重心坐标为
$$
b_i=\frac{e_i}{e_0+e_1+e_2}
$$

交点 $t$ 值为 $t=P_z=b_0P_{0z}+b_1P_{1z}+b_2P_{2z}$。

虽然说上文重心坐标的定义为面积的比值，而 $e_i$ 是有符号的面积。但此时我们已经得知 $P$ 位于三角形内部，即 $e_0,e_1,e_2$ 三者符号相同，因此这里可以不考虑符号。忽略了三角形面积为叉乘向量的模的 $\frac{1}{2}$ 也是同理。

3 光线与 bounding box 求交

Bounding box 可以看作是三组 slab 组成，每组 slab 由平行于某一坐标轴的一对平面组成。因此 Bounding box 可由两个极端点定义 pMin$(x_{min},y_{min},z_{min})$ 和 pMax$(x_{max},y_{max},z_{max})$ 。为了求光线与 Bounding box 的交点，先求光线与这三组 slabs 的交点。由于 slab 对齐坐标轴的特点，与 slab 的求交简单而高效。

光线与 Bounding box 求交算法步骤：算法开始有光线参数的有效区间设置，通常为 $(0,\infty)$。光线与每一组 slab 求交都可得到两个交点，排除掉有效区间之外的交点。可由剩下的交点进行一些比较(交点分为两类:入点和出点。求入点中的最大值、出点中的最小值，得到光线位于 Bounding box 内部的参数范围。如下图所示

求交点即解光线方程和平面方程组成的方程组，假设平面方程为 $ax+by+cz+d=0$，带入光线方程可列

$$
a(O_x+t\mathbf{d}_x)+b(O_y+t\mathbf{d}y)+c(O_z+t\mathbf{d}z)+d = 0 \
t=\frac{-d-((a,b,c)\cdot O)}{((a,b,c)\cdot \mathbf{d})}
$$
对于垂直于 $x$ 轴的一组 slab 平面的法向量都为 $(1,0,0)$ ，并且分别过点 $(x{min},0,0),(x{max},0,0)$。代入可得

$$
t=\frac{x_{min}-O_x}{\mathbf{d}x} \quad or \quad \frac{x{max}-O_x}{\mathbf{d}x}
$$
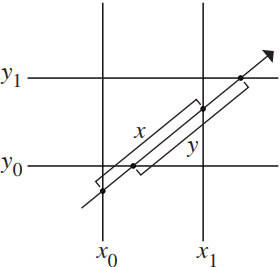
我们需要从得到的所有交点中通过一系列比较得到光线位于 Bounding box 内部的参数范围，而进行这一步骤的前提是将交点区分为两类：入点和出点。所求交点为入点 $t{near}$ 还是出点 $t_{far}$ 可由光线方向与平面法向量的关系分辨。由上述，每个 slab 的法向量都默认定义为其对应的坐标轴的正向，因此我们只需看光线方向的符号即可。

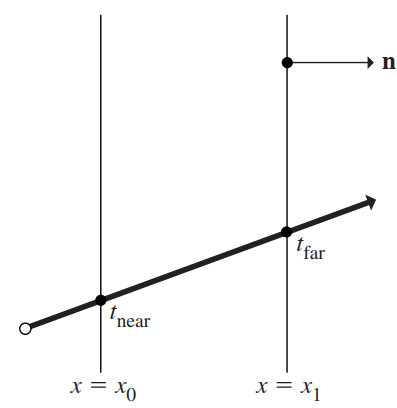
如上图所示，图中 $x_0,x_1$ 分别对应 $x_{min}, x_{max}$ ，可以看出当光线方向在 $x$ 维度为正(即与平面法向量符号相同)时，$x_{min}$ 平面的交点为入点，$x_{max}$ 平面的交点为出点。按此规则分别求出三个 slabs 的入点和出点，然后求入点中的最大值 ，出点中的最小值：

$$
t_{min}=\max{t_{near}}, t_{max}=\min{t_{far}}
$$

如果 $t_{min}<t_{max}$ 则表示光线穿过了 Bounding Box，否则表示无交点。