移动端GI
1 Summary
2 Background
基于传播的实时全局光照方法
2.1 Reflective Shadow Map(RSM) [4]
RSM 是借鉴 shadow map 的思想来近似计算间接光照的算法,这里的间接光照只考虑一次弹射情况。RSM 的核心思想是把直接光照照亮的像素作为次级光源(虚拟点光源),这些虚拟点光源区域收到直接光照,经过弹射到达着色点则得到一次反射的间接光。这里 RSM 再进行一次近似,假设次级光源都为 diffuse 材质,这样就可以忽略直接光在次级光源区域弹射的间接光在不同出射方向(到着色点的方向)的差异。
假设一个场景如下图所示
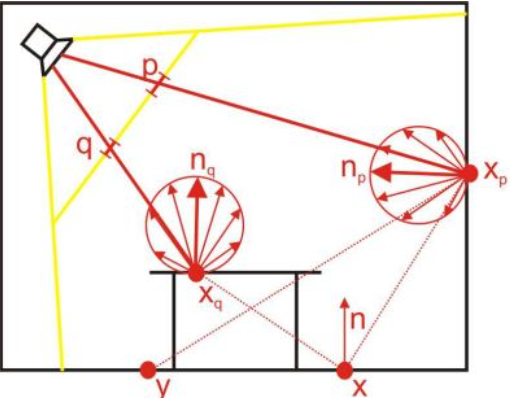
2.1.1 RSM 理论基础
将虚拟点光源所位于的像素称为 patch,那么渲染方程可以由对半球方向的积分改为对场景patch的积分,如下式变换
$$
\begin{align}
L_o(x,\omega_o)&=\int_{\Omega_{patch}} L_i(x,\omega_i)V(x,\omega_i)f_r(x,\omega_i,\omega_o)\cos\theta_i\space d\omega_i \
&=\int_{A_{patch}}L_i(x_p\rightarrow x)V(x \leftrightarrow x_p)f_r(x,x_q\rightarrow x,\omega_o)\frac{\cos\theta_x\cos\theta_p}{||x_p-x||^2}\space dA
\end{align} \label{render-equation}\tag{1}
$$
其中,$x$ 为着色点;$x_p$ 为采样的 VPL;$\theta_x$ 为 $x_p \rightarrow x$ 入射角;$\theta_p$ 为 $x_p \rightarrow x$ 的出射角。
RSM 核心思想是采样直接照亮的小 patch 作为虚拟点光源,再次发射光到像素上。这里的小 patch 就是光源视角下的shadow map像素点,将这种patch视为最小单位,其面积为积分微元 $dA$。基于此,对于上式积分,有以下两点:
积分是被积函数与积分微元乘积的求和,即 $\int f(x) \space dx = \sum f(x)\cdot dx$,因此
$$
L_o(x,\omega_o)=\sum L_i(x_p\rightarrow x)V(x \leftrightarrow x_p)f_r(x,x_q\rightarrow x,\omega_o)\frac{\cos\theta_x\cos\theta_p}{||x_p-x||^2}\cdot dA \label{sum-render-equation}\tag{2}
$$虚拟点光源为漫反射 patch,有
- VPL diffuse BRDF:$f_r=\rho/\pi$
- VPL 到着色点的出射radiance:$L_i = f_r\cdot \Phi/dA$,
其中 $\Phi$ 为 VPL 收到的辐射通量,$\Phi/dA$ 则为收到的 irradiance,乘上 diffuse BRDF 则可以得到均匀出射radiance。
将 $f_r\cdot \Phi$ 作为整体,即 VPL 的 throughput (吞吐量)
假设 $x_p$ 的吞吐量记为 $\Phi_p$ (经过BRDF),代入由VPL出发的 $L_i$ 到 $\eqref{sum-render-equation}$,可以得到着色点 $x$ 收到单个虚拟点光源 $x_p$ 的辐射强度为
$$
E_p(x)=\Phi_p \cdot\frac{\max(n_p\cdot(x-x_p))\max(n\cdot (x_p-x), 0)}{||x-x_p||^2\cdot ||x-x_p||^2} \label{direct-light}\tag{3}
$$
$\eqref{sum-render-equation}$ 中的 $dA$ 与吞吐量中的 $dA$ 抵消,同时分母中多了 $||x-x_p||^2$ 是对分子 cos 计算向量的归一化。
因此我们可以先计算 VPL 的吞吐量,再用来计算着色点的一次 bounce 间接光。
2.1.2 实现步骤
RSM 算法下的管线流程:
计算直接光照
光源看向场景,可以得到直接照亮区域,为该区域生成 RSM 所需信息,包括 位置、法线、throughput。对于 throughput,与光源类型有关:
平行光/方向光:没有衰减 $\Phi_p=c_p\cdot I$,$I$ 为光照强度(单位立体角内的光通量),$c_p$ 为 $x_p$ 点的颜色,表示不吸收该波段能量
点光源:注意点光源有距离衰减,
$$
\Phi_p=\frac{\max(n_p\cdot (v-x_p),0)}{||v-x_p||^2}\cdot I_p
$$
这里可以看出来,throughput 其实是对shadow map像素的直接光照着色结果。而每个shadow map像素的直接光照就是经过该像素patch的辐射通量,再乘上 brdf 以及余弦项的结果。可能这里就是因为像素patch,才成为 $\Phi_p$ 而不是 $L_p$?
采样 RSM,计算像素间接光
$$
L_p = \Phi_p\cdot\max(n_p\cdot\omega, 0)
$$最后像素简介光与直接光叠加起来
2.1.3 间接光 VPL 的采样方法
在 RSM buffer 中的虚拟点光源贴图中,每个像素都是一个 VPL,全部计算一次不太现实。RSM 第 2 步中,需要采样一批 VPL 计算间接光。RSM 假设屏幕空间距着色点越近的 VPL 贡献越大,采样密度随着到着色点的距离增大而减少,并且为了弥补较远 VPL 采样数越少可能会带来的问题,引入了权重,越近的权重越小,越远的权重越大,如下图所示
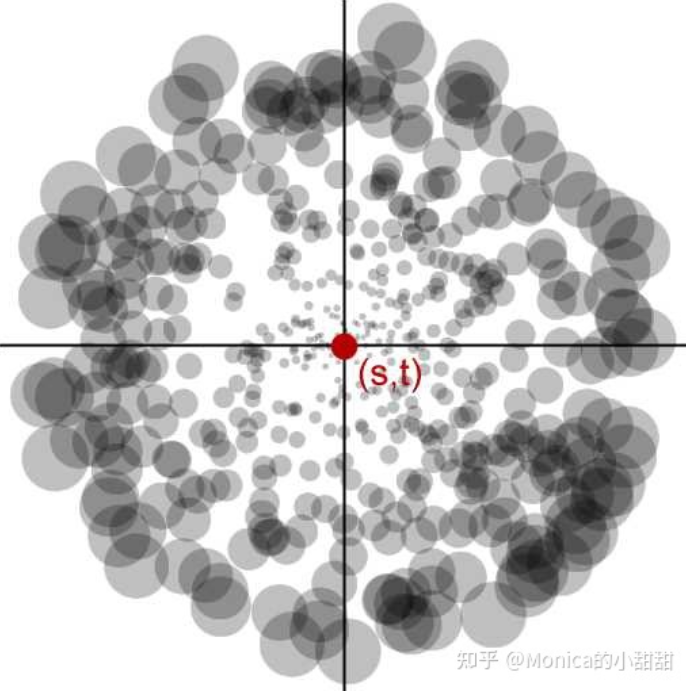
当前着色点的纹理坐标 $(s,t)$,采样范围最大半径 $r_{max}$,伪随机数 $\xi_1,\xi_2$,采样的 VPL 坐标为
$$
(s+r_{max}\cdot\xi_1\cdot\sin(2\pi\xi_2),t+r_{max}\cdot\xi_1\cdot\cos(2\pi\xi_2))
$$
$\xi_1$ 作为圆盘半径随机数,$\xi_2$ 作为圆盘角度随机数。使用 $\xi_1^2$ 作为采样权重,即距着色点的距离平方衰减。
使用上式坐标采样 RSM buffer 中 VPL,再按照公式 $\eqref{direct-light}$ 计算本次采样 VPL 的间接光照,最后乘上本次采样的权重 $\xi_1^2$。将多次采样得到的间接光进行加权和。
同时,为了降低开销,可以使用低分辨率的间接光,即 RSM 的 render target 大小采用低分辨率。在低分辨率的 RSM 使用双线性插值采样间接光。
缺点:屏幕空间采样间接光,无法处理间接光的 visibility 问题。只有一次 bounce
2.1.4 基于SSDO的可见性
前面 RSM 的计算过程中,完全忽略了VPL到着色点的可见性。这里可以借助屏幕空间AO技术来计算二者之间的可见性
2.2 Light Propagation Volume(LPV) [5]
LPV 在 RSM 的基础上,在对场景划分的体素上计算、传播间接光照。其核心思想是,对场景执行体素化,将每个体素网格中心视为点光源,将位于体素网格内的 VPL (RSM 采样得到),视为由中心发出的光,方向为中心 $\rightarrow$ VPL。基于此,可以将网格内的所有VPL间接光执行SH投影,得到SH光照编码的体素点光源。
2.2.1 SH
2.2.2 算法步骤
2.2.2.1 网格建立
采用基于 AABB 包围盒建立体素网格,即对场景模型的包围盒划分成等大小网格:
- 网格中心:
center = (CellCoord + 0.5) * CellSize + MinAABB - 已知位置 p,可以得到所属网格:
CellCoord = ivec3((p - MinAABB) / CellSize)
2.2.2.2 光照注入
将 RSM 产生的次级光源 VPL 注入到其所属网格中。
计算 VPL 所属网格
1
2
3ivec2 vpl_coord; // ...
vpl_pos = texelFetch(u_RSMPositionTexture, RSMCoords,0).rgb;
cell_coord = ivec3((vpl_pos - u_MinAABB) / u_CellSize);构建由网格中心到VPL发出的光,投影SH
1
2
3vec3 CellCenter = (cell_coord - 0.5) * u_CellSize + u_MinAABB;
vec3 centerToVpl = normalize(vpl_pos - CellCenter);
// 投影方向 centerToVpl 的 L
2.2.2.3 光照传播
光照注入过程让每个网格都生成了局部radiance信息,接下来通过传播到如下邻近网格来扩散到全局。
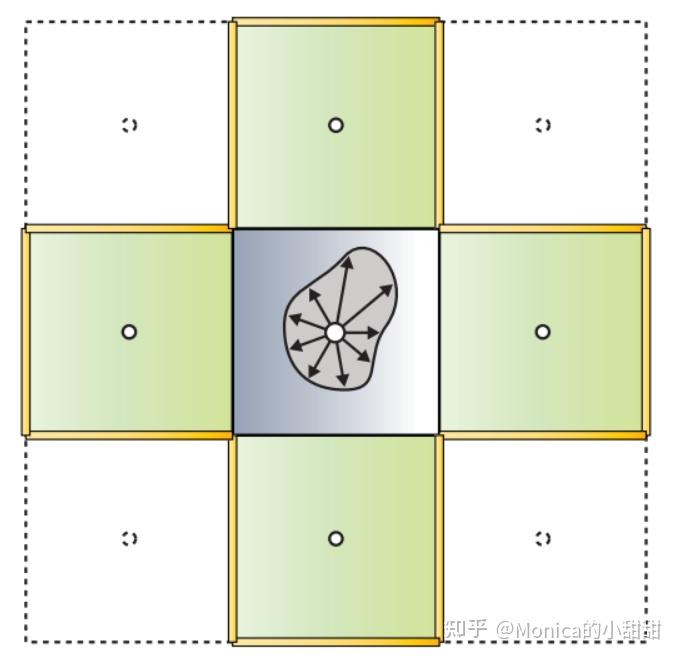
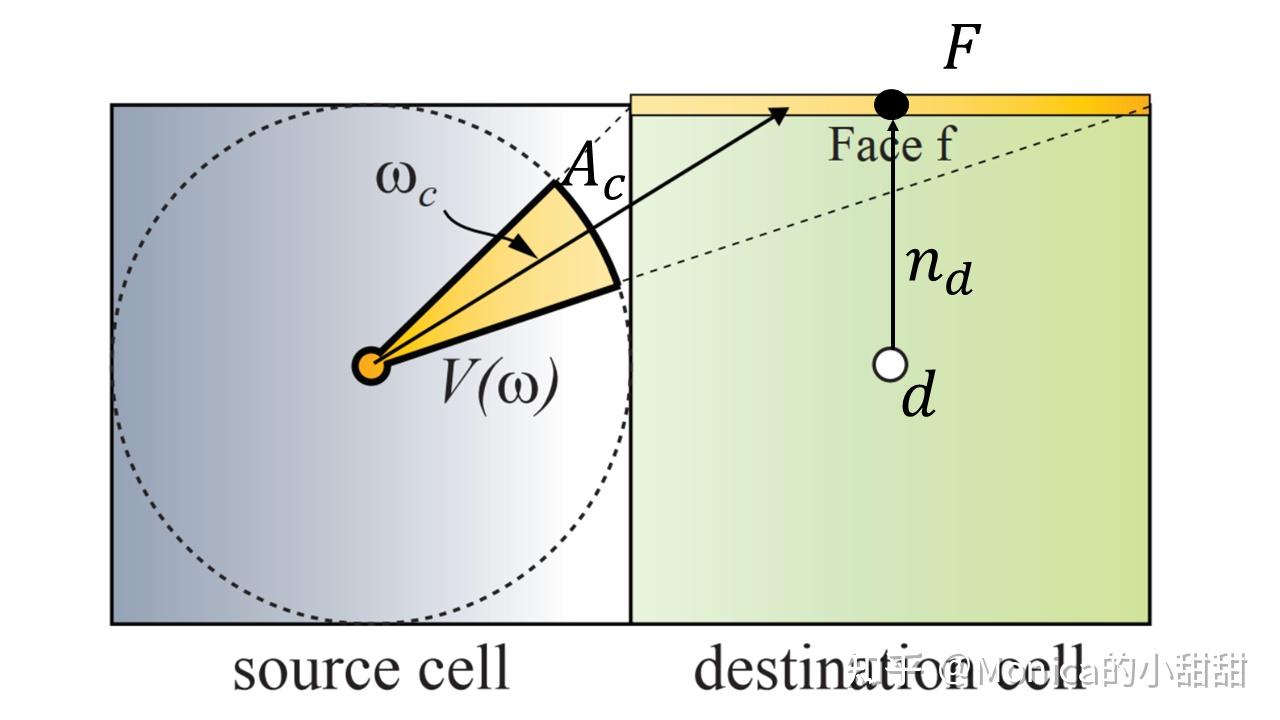
整个传播过程可以描述为:从 source cell 辐射能量到 destination cell 的五个面(注意这里不包括直接相接的那个面,这是作者定义的规则),然后以这五个面作为光源来计算 destination cell 中心点 d 接收到的 Irradiance $E(d,n_d)$,再更新其球谐系数 $L_l^m$ 即可。
- 先从 source cell 的SH中,得到 $\omega_c$ 方向上的outgoing radiance $L(\omega_c)$
- 作者将 F 表面接收到的辐射通量直接作为网格中心 d 向外的radiance, $L_{f}(-n_d)=L(\omega_c)\cdot A_c$,其中 $A_c$ 为立体角对的面积
- 将 F 面光源的光照编码进网格中心点的SH,直接投影到 $n_d$ 方向得到系数,然后与现有系数累加
3 Local Radiance Transfer

3.1 局部 GI
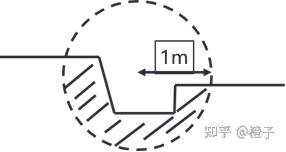
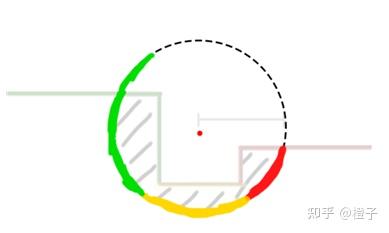
在某一个小空间内,如下图1米半径的空间内,考察它的GI性质。更进一步的,我们可以把这个复杂的空间内的反弹操作近似成对一个这样的球空间的操作:
References
[2] GI from Local Radiance Transfer
[3] 一篇文章搞懂Light Propagation Volumes(LPV)算法及其实现细节
[4] 【论文复现】Reflective Shadow Maps
[5] 【论文复现】Cascaded Light Propagation Volumes for Real-Time Indirect Illumination