1 Summary
这篇论文提出了一种基于light probe的全局光照方法,其中包括预计算过程中probe数据的生成方式、基于probe数据的光线追踪算法以及实时渲染中的着色过程。
在预计算过程中,对场景的每个离散采样点生成以该位置为中心的probe数据,每个probe包含了球面分布的两组数据:probe中心收到每一方向上最近点的radiance、该最近点的法线以及该最近距离(radial distance);为了处理diffuse间接光,对probe中心收到的radiance进行prefilter得到的irradiance、最近距离及其平方。
同时,probe数据采用了具有分段线性投影特性的octahedral map存储,作者提出了在基于此map的具有2-level层级加速的高效光线追踪算法。为了得到确定的求交结果,需要在着色点周围的八个probe中选择进行求交测试,为此,作者提出最小化octahedral map访问次数的选取策略。
在实时渲染的着色过程中,直接光照选择采用传统的deferred shading。对于间接光照,作者将BRDF拆分为Lambertian项和glossy项,并为每一项采样一条光线计算间接光照:前者由于其在分布空间变化平缓的特性,而选择采样irradiance map,并可以使用较大的filter进行降噪;而后者在其分空间变化强烈,采样radiance map,并使用较小的filter降噪。而对于降噪filter过程,除了应用传统的空间与时序的降噪,作者还提出使用probe中的几何信息来构建geometry-aware的权重,来避免light/shadow-leaking问题。
作者源码 [3]
2 Light Field Probe Structure
Light Field(光场)描述了空间中一点的radiance在出射方向上的分布,假设点 \(\mathbf{x}\in \mathcal{R}^3\),以及该点的一个出射方向 \(\omega\in \mathcal{S}^2\) (应该指上半球),那么Light Field可使用 \(\mathcal{L}(\mathbf{x},\omega)\) 表示。不可能对场景中每一点都定义Light Field,作者通过将场景的包围盒均分为grid来将空间离散化,对每个grid的一个采样点定义一个light field。
在每个离散采样点 \(\mathbf{x}'\)(每个grid的一个采样点)上存储一个球形light field probe数据,用以记录点 \(\mathbf{x'}\) 的每个方向 \(\omega\) 的数据,包括:
- \(\mathcal{L}(\mathbf{x'},\omega)\):点 \(\mathbf{x}'\) 在方向 \(\omega\) 的入射radiance。light field是在球面上的定义,而probe像素有一定大小,可以看作在球面上一片的radiance,因此文中称为spherical light field slice radiance。
- 在方向 \(\omega\) 上距点 \(\mathbf{x'}\) 最近的点 \(\mathbf{x''}\) 的表面法线:\(\vec{\mathbf{n_{x''}}}\)
- \(\mathbf{x'}\) 与 \(\mathbf{x''}\) 之间的radial distance \(r_{\mathbf{x'}\leftrightarrow\mathbf{x''}}\)
2.1 Probe 数据生成方式
上述Probe数据中的几何信息,例如 \(\vec{\mathbf{n_{x''}}}\)、\(r_{\mathbf{x}'\rightarrow\mathbf{x''}}\),作者使用光栅化管线生成。而spherical light field slice radiance \(\mathcal{L}(\mathbf{x'},\omega)\) 需要光线模拟过程来生成:可以通过光栅化过程现有的着色技术(deferred renderer with shadow map)来计算;或者使用离线path tracer;作者选择迭代应用本文提出的着色算法来生成,具体做法:对于一次反射的直接光照 \(\mathcal{L}(\mathbf{x'},\omega)\) 只包含场景中光源的发光,重复应用着色算法得到具有额外反射的 \(\mathcal{L}(\mathbf{x'},\omega)\)。
2.2 实现细节
一个probe本质上是以其中心点 \(\mathbf{x'}\) 为球心的球面上所有方向的信息,类似于全向相机的渲染(Omnidirectional),其数据组织为cube map的形式,每个像素的数据为其对应方向 \(\omega\) 的probe数据。本文提出的算法中不直接使用cube map,而是在生成probe数据过程中,将cube map重采样到octahedral map(oc-map)中 [1] [2] [5.1],之后的算法就不再需要cube map。八面体参数化是将球面映射到一个方形平面上,相比于cube map,oc-map具有优势:失真度更低;同等质量水平下,存储开销与带宽降低4倍;分段线性的投影能够应用于高效的ray marching。
每个probe的oc-map数据作为2D texture array的一个layer存储,一个oc-map像素大小为32字节,其存储格式为:
- HDR radiance \(\mathcal{L}(\mathbf{x'},\omega)\):R11G11B10F (32 bits/pixel)
- 法线 \(\vec{\mathbf{n_{x''}}}\):RG8 (16 bits/pixel)
- radial distance \(r_{\mathbf{x}'\rightarrow\mathbf{x''}}\):R16F (16 bits/pixel)
irradiance probe:很多着色过程得益于prefilter light field radiance \(\mathcal{L}(\mathbf{x'},\omega)\),因此将prefilter结果预存储到一个cosine-weighted incident irradiance probe \(\mathbf{E}(\mathbf{x'},\vec{\mathbf{n}})\),即点 \(\mathbf{x'}\) 处的法线方向 \(\vec{\mathbf{n}}\) 上收到的radiance积分。例如,Lambertian项描述的漫反射项。作者发现irradiance probe的oc-map的分辨率高于 \(128\times 128\) 后就不会再有精确度方面的收益了。irradiance probe的数据存储格式和上述基本相同,只是将radiance替换为irradiance,法线替换为radial distance的平方,之后用于降噪过程的切比雪夫测试。
radiance probe需要的分辨率取决于渲染分辨率和场景中的最低粗糙度,避免完美镜面反射的走样。为此需要满足八面体纹素对着的立体角不大于probe中心位置的像素对着的立体角。文中建议1024x1024的分辨率。
场景中不同区域在屏幕上的像素比例不同,例如离相机远的区域占用像素更少、粗糙度越低对应的立体角越小。如果probe分辨率不足,会导致八面体纹素对应的立体角大于像素对应的立体角,像素采样到的radiance信息超出了像素范围,即radiance采样率不足。
3 Light Field Probe Ray Tracing
已知光线方程 \(\mathbf{p}(t)=\mathbf{r}_o+t\cdot\mathbf{r}_d\),求解最近交点 \(\mathbf{p}(t')\equiv\mathbf{p}'\)。Light field probe中的几何信息radial distance和法线用于解决incoherent世界空间求交,radiance probe和irradiance probe包含了所需的辐射量,交点处的出射radiance \(\mathcal{L}(\mathbf{p}',-\mathbf{r}_d)\)和入射irradiance \(\mathcal{L}(\mathbf{p}',\vec{\mathbf{n}}\equiv\vec{\mathbf{r}_d})\)。
作者提出的Light Field ray trace过程如下图:先选择一个候选probe,执行single-probe ray trace,当得到miss或hit结果时,则求交结束。当无法得到求交确定结果时,选择下一个候选probe继续执行single-probe ray trace。
如果得到不确定的结果,则表示本次选择的probe缺少光线传播区域的信息,例如从probe视角来看,光线传播区域被遮挡,因此无法确定是miss或hit。


作者提出的 light field ray tracing算法主要包括两方面:选择候选probe的启发式策略;probe的oc-map中的光线求交。
3.1 Single-Probe光线求交
球面的八面体投影性质:将三维空间的线段映射为oc-map中的多段线(最多4段线),其中每段线分布在oc-map的不同面;probe的三维球体被以probe中心为原点的坐标系分割成8个平面,分别对应了oc-map的8个面,而每段线的端点为三维空间的线段与三个坐标轴对齐面的交点在oc-map的投影。
probe的光线求交:首先计算出光线在oc-map投影的几组端点;然后沿着线段进行ray-march,使用当前位置与probe中心的radial distance \(t_0\) 以及当前位置在oc-map中的对应纹素存储的radial distance \(t_1\) 做求交测试,
- 如果 \(t_0>t_1\) 表示光线交于一个表面(hit)或者从一个表面后面通过(unknown,光线行进区域在probe中被遮挡)
- 否则miss
probe的光线求交与SSR思想类似,不同的是:
- 光线在depth buffer中的投影是一条直线,而在oc-map中的投影是几段线
- 对于光线行进位置处的求交测试:SSR使用相机视角的depth buffer在行进位置处的深度值与相机到行进位置距离,而本文的probe求交则使用oc-map在行进位置处的radial distance与probe中心到行进位置的radial distance
对于oc-map的一个面内ray-march可以使用hierarchy算法加速 [4]。上述求交测试中,当 \(t_0 < t_1\) 可以确定miss,但 \(t_0 > t_1\) 有可能hit,也有可能从后面通过(unknown)。为了得到确定结果,需要确定求交平面即oc-map的对应texel在三维空间的范围。oc-map的每个纹素描述的是距离probe中心 \(r_{\mathbf{p}'\leftrightarrow \mathbf{x}''}\) 并且法线为 \(\vec{\mathbf{n_{x}}''}\) 的一个小patch(surfel)。基于法线和表示精度,作者使用一个球形体素包围该patch。只有当前行进点与该体素相交时,才表示与光线与patch表面相交。法线也可以用作排除掉相对于光线方向的背面的交点。下图为光线求交过程的可视化,光线在如图oc-map投影得到三个线段
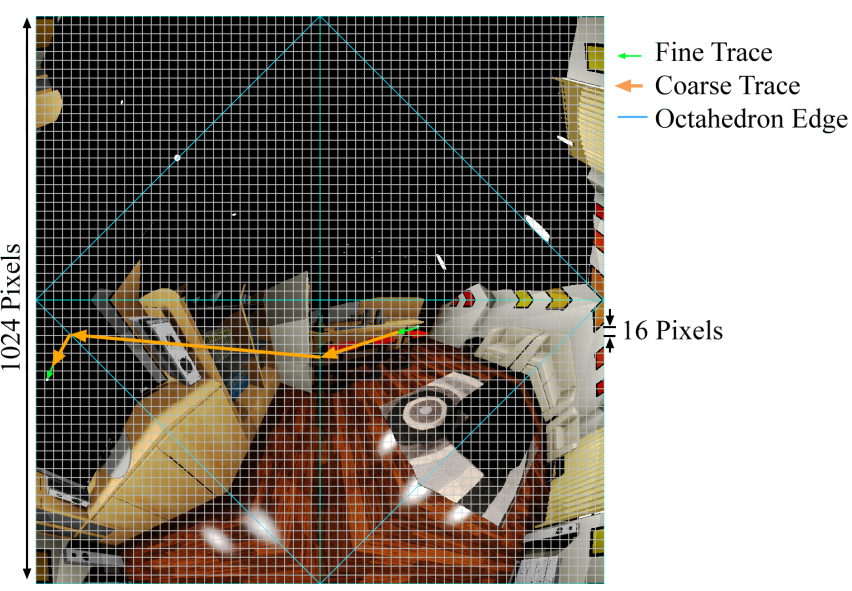
3.2 Probe选取策略
对于任意光线起点 \(\mathbf{r}_o\) 都会被其周围8个probe所描述立方体包裹,如下图中编号所示。light field ray tracing首先选择中心距光线最近的probe进行求交。根据空间局部性原理,这8个probe往往具有相似的visibility信息,这一启发策略在深度高复杂高和probe密度低的情况下会失效。而首先选择最近的probe是因为光线在该probe的oc-map中的投影最短,这样会带来ray-march过程中访问texture的次数较少;同时,最近的probe更可能观察到光线行进区域而不被遮挡。
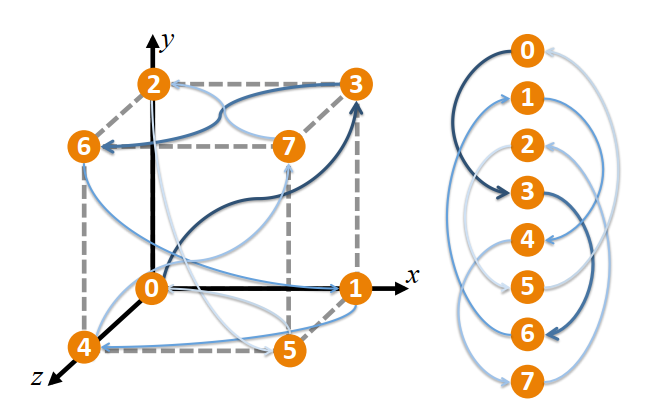
当single-probe hierarchy ray march不能确定求交结果时,需要再选择一个probe执行求交过程。首先将光线起点移动到上一个确定求交结果的行进位置,\(\mathbf{r}'_{d}=\mathbf{r}_o+t'\mathbf{r}_d\) 。如果新的光线起点进入了一个新的立方体范围,那么再次选择一个距离光线最近的probe。如果新的光线起点还在原立方体范围内,从未进行求交测试的probe中选择一个距离上一个probe最远的probe,这种策略同样是基于空间局部性原理。为此,作者设计了简单高效位运算,假设light field ray tracing始于距光线最近的probe \(i\),那么下一次选择 \(i'=(i+3)\space mod\space 8\),选择顺序如上图的有向曲线所示。
图3.3使用像素颜色表示了该像素得到求交结果的probe编号,同样的颜色表示同一个probe。可以看出越近的像素,其遮挡信息越相近。注意:probe的选取策略只会影响性能,不会影响求交结果。

3.3 性能说明
由于文中提出的probe选取策略会得到光线在所选probe的oc-map中的投影线段最短,而投影线段的缩短减少光线行进的步数,也就是减少oc-map的访问以及求交测试。这可以带来便利的内存-性能权衡:增大probe密度不仅能够提高准确度,也会由于缩短光线在oc-map的投影长度而提高性能。
在实现上,作者通过重新组织glsl中的branch,降低线程动态分支的开销。light field ray tracing使用two-level mipmap实现的层级加速,第2层分辨率是上一层的 \(1/16^2\)。
4 Shading with Light Field Probes
原始的着色算法:光栅化直接可见表面后(deferred shading)在pixel shader中使用shadow map计算直接光照;然后在同一pixel shader中进行蒙特卡洛积分来估计间接光:基于重要性采样,发出 \(n\) 个随机光线,每条光线对light field进行采样得到对应入射方向上的incident radiance。最后乘上cosine-weighted BRDF并使用采样分布和采样数 \(n\) 归一化后得到积分估计。
上述原始算法可以捕获到静态和动态物体的间接效果,同时可以使用该算法再次渲染probe来逐步填充light field probe的在任意次反射之后的radiance分布。但该方法有两个局限:
更高阶间接光照效果的视点偏差:当从light field probe中采样radiance时,得到的是采样点到probe中心的radiance,与着色点是有一定差距的。
在使用上一章节描述的光追算法,得到采样光线的反射点后,可将probe中心点到反射点的方向进行转换得到对应的oc-map的采样坐标,采样radiance map得到的是probe中心收到反射点的入射radiance。
性能:原始算法中需要很多光线数量来降低噪声,无法应用到实时渲染中
但更高阶的光照效果的失真影响远远小于第一次反射,作者更关注性能问题。作者对原始着色算法进行近似与优化,使其更适用于现代实时渲染管线。
4.1 Spatial-Temporal Radiance Denoising
实时渲染下能够支持的光线数量非常有限,应对噪声的通常做法是使用时序-空间上的降噪,即SVGF的思想。针对BRDF,作者将其分解为两项:描述diffuse的Lambertian项和描述specular的glossy项。间接光照的render pass为每一项采样(cosine-weighting)一条光线,并将结果写入带噪声的Lambertian和glossy入射radiance buffers。之后再在单独的denoise pass进行双边过滤(cross-bilateral)和时序重投影降噪。
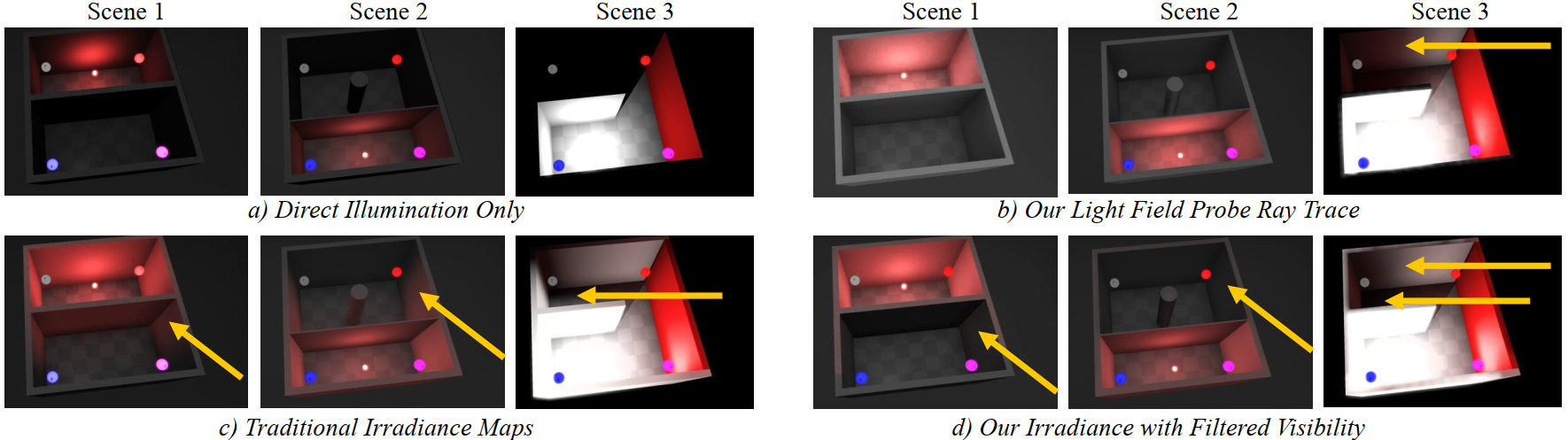
对于Lambertian项,均匀分布在法线方向的上半球范围,同样采样率水平下,噪声更大,但变化较小。因此可以直接采用存储积分后的irradiance,同时由于其变化较为平缓的特点,可以使用更大的filter,文中采用半径为12像素、步长为2像素的空间滤波与98%置信度的时序滤波。glossy项虽然噪声较小,但变化较为剧烈,因此使用更小的filter,采用半径为3像素的空间滤波与75%置信度的时序滤波,如 图4.1 所示。

4.2 Irradiance with (Pre-)Filtered Visibility
前文所述的预计算过程,通过蒙特卡洛计算radiance积分估计,得到probe中心位置的irradiance oc-map(128X128)中,采样坐标为法线方向转换得到oc-map坐标。在运行时,作者通过在如图3.2的八个probe之间使用三线性插值来估计着色点处收到的irradiance。但该方法存在的缺陷:插值得到的irradiance会透过irradiance probe立方体网格体积内的物体,从而造成漏光或者漏阴影,如图4.3所示。具体而言,在立方体网格体积内的着色点与一个或多个probe之间的可见性假设是无效的。
为此作者提出了一种geometry-aware方法来避免这些不合理现象。在预计算cosine-filtered irradiance map时,采用cosine-power lobe的滤波方式,对radial distance和其二次方进行滤波得到的filter map,这中滤波方式避免了距离的离散值带来的锯齿,同时又不造成过度模糊,如图4.2所示。在运行时,结合基础的三线性插值的权重与额外的两项得到geometry-aware权重:
- 着色点表面法线与其到probe的方向之间的clamp dot
- local radial distance分布的切比雪夫可见性检验,方法与VSM[5]原理类似,分布方差为 \(\sigma^2=E[r]^2-E[r^2]\)。
最后累加结果使用8个probe权重之和归一化。

5 Appendix
5.1 八面体参数化
cube map的八面体参数化过程:先将球面投影到正八面体上,然后再投影到 \(z = 0\) 平面上,并将 \(z < 0\) 的部分进行翻转,最终形成一个二维正方形。如下图所示
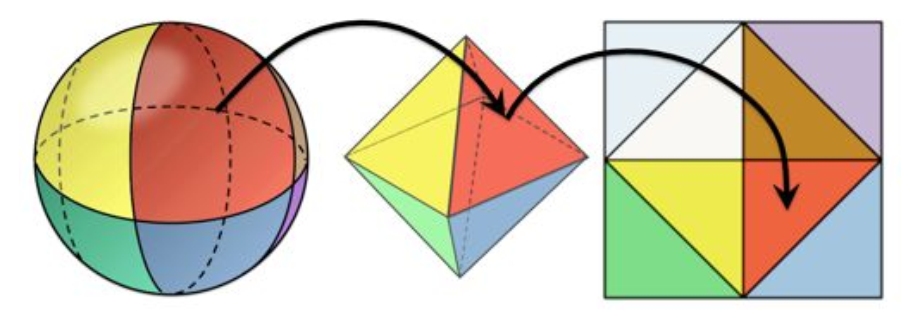
Reference
[1] Cigolle, Zina H., et al. "A survey of efficient representations for independent unit vectors." Journal of Computer Graphics Techniques 3.2 (2014).
[2] https://zhuanlan.zhihu.com/p/384232048
[3] https://github.com/Global-Illuminati/Precomputed-Light-Field-Probes
[4] McGuire M, Mara M. Efficient GPU screen-space ray tracing[J]. Journal of Computer Graphics Techniques (JCGT), 2014, 3(4): 73-85.
[5] William Donnelly and Andrew Lauritzen. 2006. Variance shadow maps. In Proceedings of the 2006 symposium on Interactive 3D graphics and games (I3D '06). Association for Computing Machinery, New York, NY, USA, 161–165.